
式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
*問題は追加していく予定です。多項式の計算 多項式と単項式の乗除 乗法公式 式の展開と加法、減法 因数分解の基本 因数分解ーいろいろな計算 因数分解 係数の組み合わせ 計算の工夫 素因数分解多項式の計算の利用 式による証明 図形への利用多項式の計算のまとめ まとめの問題平方根中学3年生 数学 平方根の加法・減法 問題プリント 無料ダウンロード・印刷 √の中が等しい数は、文字式の同類項と同じように分配法則を使ってまとめることができることなどについて理解し、平方根の加法・減法を練習する問題プリントです。
式の計算の利用 中3 応用問題
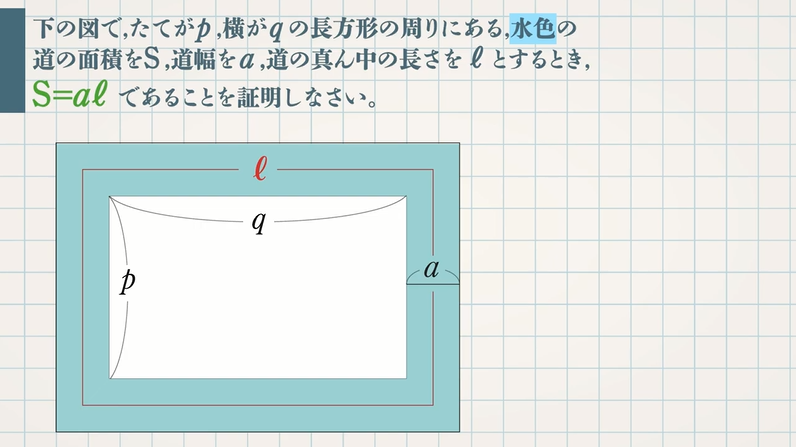
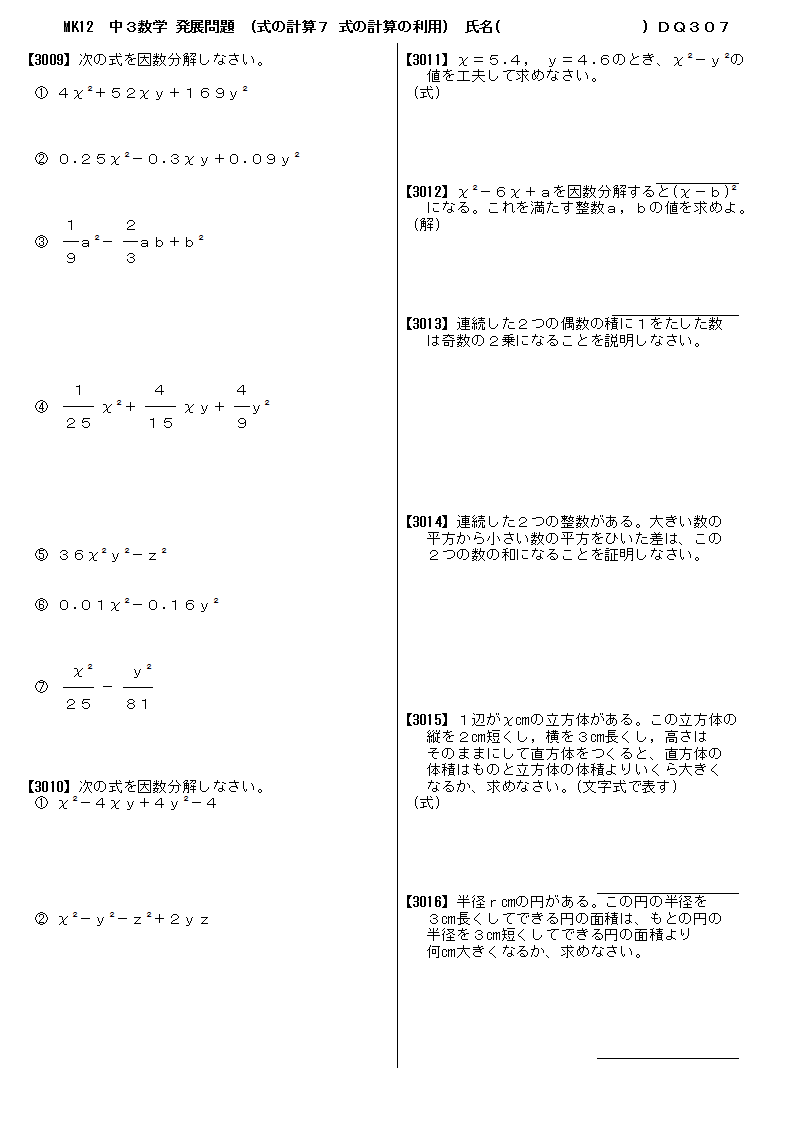
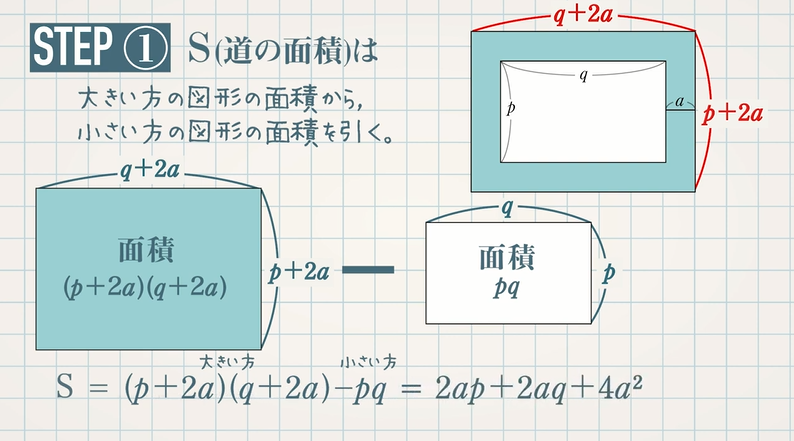
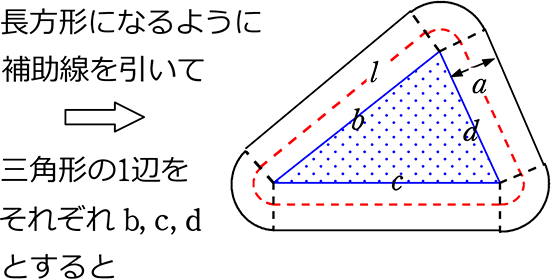
式の計算の利用 中3 応用問題-今回は中3で学習する式の計算の利用から 「円、正方形の図形に関する証明」 を解説していきます。 取り上げるのは、こういった図形の問題です。 難しそうに見える問題だけど、 手順を覚えてしまえば簡単に解くことができるようになります! という第1章 式の展開と因数分解 <前: L7 因数分解(3)‐乗法公式の利用2 の問題 L8 式の展開・因数分解の利用 の解答 :次> 練習問題1 連続する2つの偶数の積に1をたすと、その2つの偶数の間の奇数の2乗になる。 このことを証明しなさい。 練習
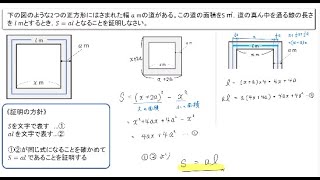
中3 式の計算の利用 円 正方形の図形の証明をイチから 数スタ
3章 1次方程式 2.1次方程式の応用 1方程式を利用した文章題の解法の手順 ①問題をよく読み、わからない数量を\(x\) とおく。 ②等しい数量の関係をみつけて、方程式を作る。 ③方程式を解く。 ④方程式の解が問題に適しているか確かめる。解き方の手順を考えよう 手順① 追いつくまでの時間を文字で置く 手順② それぞれの道のりを文字で表す 手順③ 方程式を完成させて解く 練習問題で理解を深める! 何分で追いつくか? のまとめ 中3受験生へこの力を身につけたら本番で60点は今回は塾生から質問があった問題の解説をまとめました。 同じような疑問を持っている人も多いと思うので参考にしてみてくださいね^^ 因数分解の応用問題 多項式・因数分解の応用問題は様々な問題が
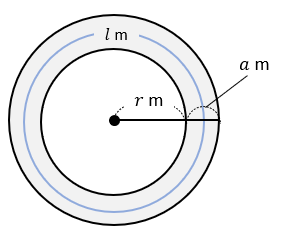
掛け算の計算の応用問題 小学3年生で学習する掛け算の計算問題で、 こちらのプリントは小学2年生の掛け算と比較して、より高度な応用問題となっています。 しかし2年生までの計算問題を順当にこなしていれば、そこまで難易度の高い単元ではありませ 中1数と式 一次方程式 基本一次方程式の利用(比例式) 19年5月29日 ここでは、一次方程式を利用して解く問題を見ていきます。比の復習をした後、比を使った問題を考えていきます。 目次 比;3 式の計算 式の計算の利用 01 JM04Z2K102 ,左ページの「Point」を確認しながら,次の問題を解いてみましょう。 ⑴ x =な24 のとき,( x 3 )( x 7 ) x( x 11 ) の値を求めなさい。 ⑵ 半径86 m の円形庭園 中に 14 池がある。 このとき,池の面積をのぞいた庭園の面積を求めなさい。ただ し,円
式の計算の利用 中3 応用問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 | ||
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「式の計算の利用 中3 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
式の計算 例題 同類項をまとめる 多項式の加法・減法 縦の計算 多項式と数の乗法除法 分配法則と加法減法 分数形の加法・減法 乗法 累乗 除法1(整数) 除法2(分数) 乗法と除法の混ざった計算 式の値 式による説明(2つの連続する奇数・・・) 式による説明(2けたの自然数・・・) 式による説明(奇数式の計算 式の計算の利用 JM04Z2L134 JM04 35 5 ⑴ 126 を素因数分解すると 126 = 2 × 32 × 7 これに正の整数 n をかけて,ある正の整数の 2 乗にするには 126 × n = 2 × 32 × 7 × n より,2 × 7 × n が正の整数の 2 乗になればよい。 よって,求める最も小さい正の整数 n は
Incoming Term: 式の計算の利用 中3 応用問題,




0 件のコメント:
コメントを投稿