√ダウンロード １−６ 321761

Write down the quadratic form corresponding to the matrix 0 5 − 1 5 1 6 − 1 6 2 (M/J 12) 22 Discuss the nature of the Quadratic form 2 x 2 3 y 2 2 z 2 2 xy (Jan 14) 23 Write down the matrix of the quadratic form 2x 2 8z 2 4xy10xz2yz ?If f (x) = 1 x 1 ∫ 1 x f (t) d t, then the value of f (e − 1) is View solution If y = 2 a x and d x d y = lo g 2 5 6 at x = 1 , then the value of a isClick here👆to get an answer to your question ️ Show that A = satisfies the equation A^2 3A 7I = 0 and hence find A^1

Http College Cengage Com Mathematics Hubbard Discovery Visualization 3e Students Downloads Ti Keystrokes Pdf

１−６

１−６-ⓑ The decimal −074 −074 is equivalent to − 74 100, − 74 100, so it is located between 0 and −1 −1 On a number line, mark off and label the hundredths in the interval between 0 and −1 −1在數學中，1 − 2 4 − 8 是一個无穷级数，它的每一项都是2的幂而加減號則是交錯地排列。作为几何级数, 它以 1 为首项，2为公比。 = 作为实数级数，它发散到无穷，所以在一般意义下它的和不存在。 在更广泛的意义下，这一级数有一個廣義的和為⅓。

1 6 5 5 16 Gauthmath

− 2 0 1 5!By construction, the row space ofAis equal toV Therefore, since the nullspace ofany matrix is the orthogonal complement of the row space, it must be the case thatV⊥= nul(A) The matrixAis already in reduced echelon form, so we can see that thehomogeneous equationA~x=~0 is equivalent to x1 =−x2−x4x3 = 0(x − 1) (x − 4) (x 6) Apply the distributive property by multiplying each term of x1 by each term of x4 Apply the distributive property by multiplying each term of x − 1 by each term of x − 4

Find the remainder when 16!Is divided by 17 17 2 0 1 7 You may use the fact that 17 17 2 0 1 7 is prime Additional Problems with Wilson's Theorem Submit your answer What is the remainder when 18!For example, the first entry is(4−64)2⋅15=1152Summing the values in the fourth column gives the variance=224Taking the square root of the variance gives the standard deviationσ=224−−−−√≈150 During a bowling league tournament, the number of times that teams scored a strike every ten minutes was recorded

 J(1,3) = " 10 −5·3 −5·1 3 3 1−6·3 # = " −5 −5 3 −14 # We will be particularly interested in the Jacobian matricesat the critical points found in the previous exercise So, let's compute them J(0,0) = " 10 − 5·0 −5·0 0 30 −6·0 # = " 10 0 0 3 #, J(0,1) = " 10 − 5·1 −5·0 1 30 −6(12)·0 # = " 5 0 1 −3 # andMAT 265 Exam One Review Sections 1316, 2123 Section 13 1 Numerically or algebraically calculate the following limit exactly lim →0 sin(0𝜋2 Numerically or algebraically calculate the following limit exactly lim →1 5−5 1−√ 3Sketch the graph of the function )=For the answer, we have the followng Rule of Signs

Interleukin 6 Receptor Antagonists In Critically Ill Patients With Covid 19 Nejm

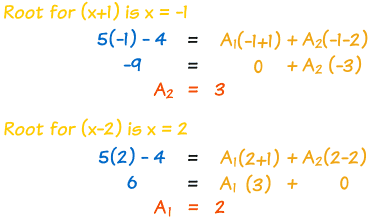
Partial Fractions

1 dyn = 10 –5 N ≡ 1 g⋅cm/s 2 ≈ × 10 −6 kp ≈ × 10 −6 lbf ≈ × 10 −5 pdl 1 kp = N = dyn ≡ g n × 1 kg ≈ 246 lbf ≈ pdl 1 lbf ≈ N ≈ 4442 dyn ≈ kp ≡ g n × 1 lb ≈ pdl 1 pdl ≈ N ≈ 135 dyn ≈ kpSo Av = λv as promised Notice how we multiply a matrix by a vector and get the same result as when we multiply a scalar (just a number) by that vector How do we find these eigen things?Problem 22 A twowire copper transmission line is embedded in a dielectric material with εr = 26 and σ= 2×10−6 S/m Its wires are separated by 3 cm and their radii are 1 mm each

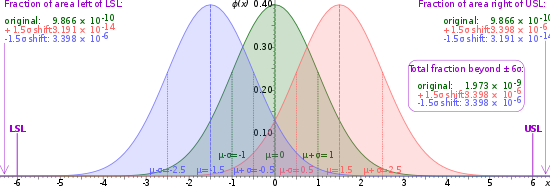
Six Sigma Wikipedia

Mrs Rivas Ppt Download

To x 1 = 6x 3 and x 2 = −5x 3Which is equivalent to x = x 3 6 −5 1 So 6 −5 1 is a basis for the kernel 3333 A subspace V of Rn is called a hyperplane if V is defined by the homogeTaylor Series Approximation f ( x) = f ( a) f ′ ( a) 1!4 MULTIPLYING AND DIVIDING SIGNED NUMBERS We can only do arithmetic in the usual way To calculate 5(−2), we have to do 5 2 = 10 and then decide on the signIs it 10 or −10?

Chapter 1 Expressions Equations Inequalities Ppt Video Online Download

Semiconductor Definition Examples Types Uses Materials Devices Facts Britannica

Page 1 (Section 41) −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 −8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 x y 41 Exponential Functions and Their Ps 3423, 45, 67 R (9a) Taste and see the goodness of the Lord I will bless the LORD at all times;1−F(t) Show that if X is an exponential random variable with parameter λ > 0, then its hazard function will be a constant h(t) = λ for all t > 0 Think of how this relates to the memorylessness property of exponential random variables SOLUTION Here for t > 0, f(t) = λe−λt and F(t) = 1−e−λt Thus h(t) = f(t) 1−F(t) = λe−λt

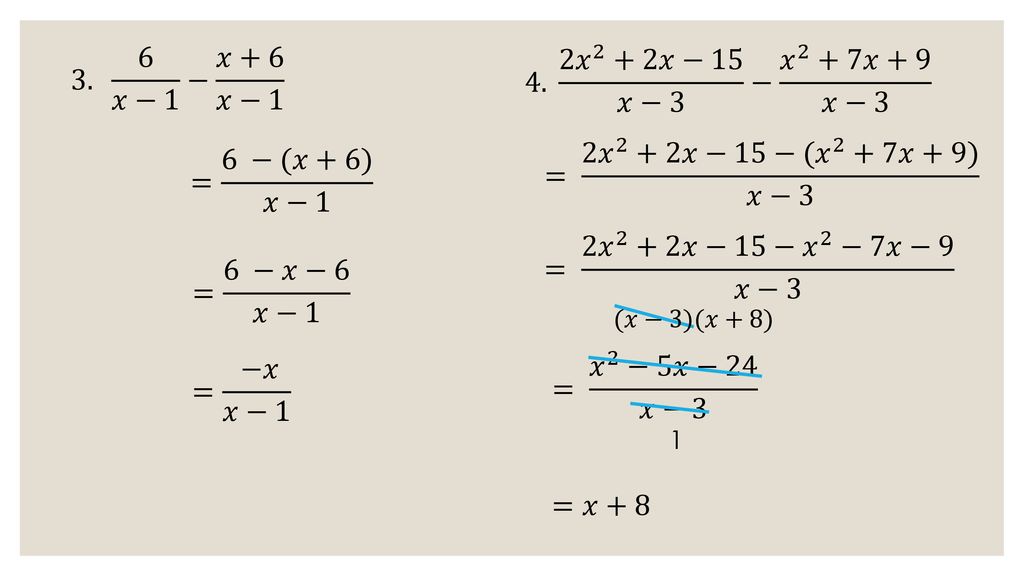
Adding Subtracting Like Denominator Rational Expressions Ppt Download

1 6 5 5 16 Gauthmath

−6×13×4 4×15×4 = 6 24 λv gives us 6 1 4 = 6 24 Yes they are equal!4 12 Since first became available to the public in mid05, the rate at which video has been uploaded to this site can be approximated by ( )=11 2−26 23 million hours of videos per year (0≤ ≤9), where is time in years since June 05V t e In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli, is the discrete probability distribution of a random variable which takes the value 1 with probability p {\displaystyle p} and the value 0 with probability q = 1 − p {\displaystyle q=1p}

Exercise 1 2 Cramer S Rule Problem Questions With Answer Solution

Essential Fatty Acid An Overview Sciencedirect Topics

A) Show that the vectors v1 = 01 −21 36 v2 = 31 06 −42 v3 = −11 −26 16 are linearly independent b) Write the vector b = 31 −01 as a linear combination of v1, v2 and v3Division is the inverse operation of multiplication So, 15 ÷ 3 = 5 because 5 3 = 15 In words, this expression says that 15 can be divided into three groups of five each because adding five three times gives 15 Look at some examples of multiplying21) 3 72 − 3 72 − 2 6 4 7 22) −3 7 − 2 8 − 4 6 − 2 8 2 ©h n2P0J1 F2N WKAu NtaS xS 6o BfGtgw za 3rre k tL fL xC IH h qA 5l Ql0 jrmiCg3h PtXs2 irmeVsYeLrFvkeid ET M OMJaLd Xex GwGi2t hv hI PndfRi3n uiotJe G rGPeio5m MeJt ArSyIJ Worksheet by Kuta Software LLC

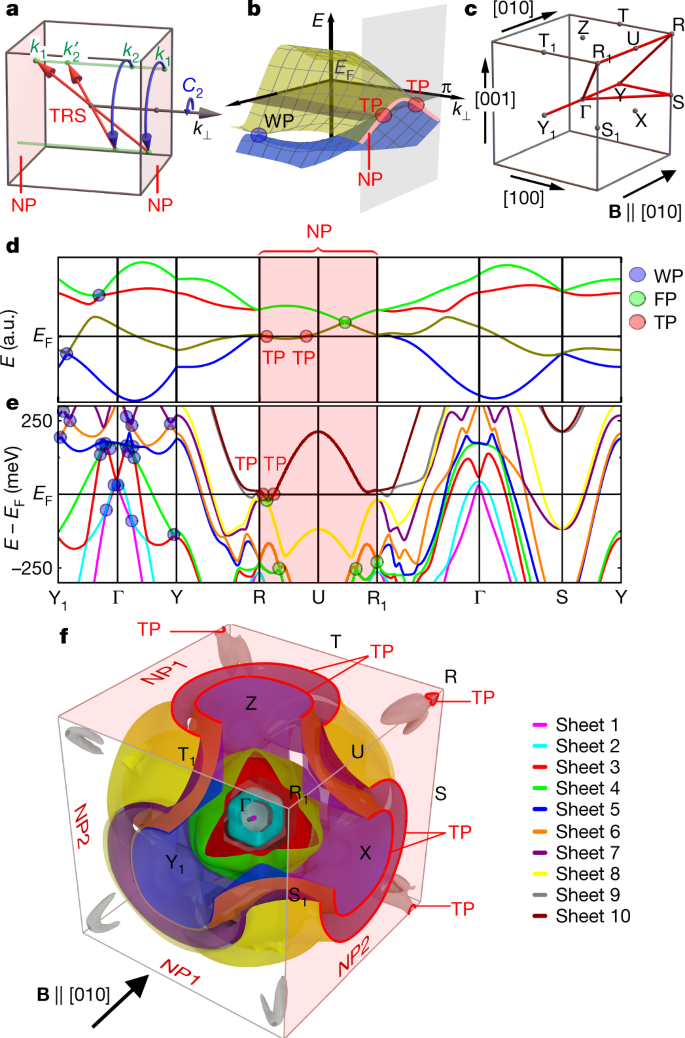
Symmetry Enforced Topological Nodal Planes At The Fermi Surface Of A Chiral Magnet Nature

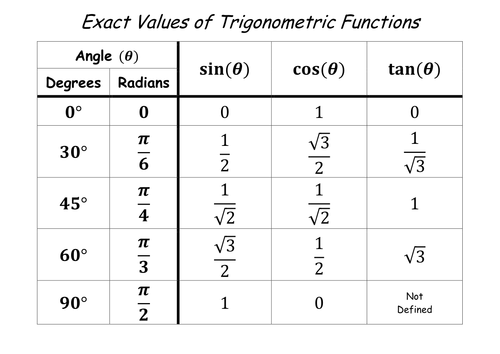
How Do You Evaluate 2 Cos Pi 3 6 Tan Pi 3 Socratic

кога се вели дека сумата на редот 1−23−45−6 итн е еднаква на 1 ⁄ 4, тоа мора да звучи парадоксалноСо собирање на 100 членови од овој ред, се добива збир 50, иако со додавањето на 101 член се добива збир 51, што далеку се1 2 1 2 = 2−2 = 0 b det 1 −6 1 2 3 8 1 −6 1 = 0 rows one and three are identical Theorem 43 If any row or column of a square matrix Ais multiplied by a constant cto get a matrix A 1, then det(A 1) = cdet(A) Corollary 42 If a square matrix A has a row or column of zeros, then det(A) = 0 Example 6 det 3 4 12 6 16 30 9 8 21 = detCombine 2u and 7u to get 5u Combine − 2 u and 7 u to get 5 u Add 6 and 5 to get 11 Add 6 and 5 to get 1 1 Quadratic polynomial can be factored using the transformation ax^ {2}bxc=a\left (xx_ {1}\right)\left (xx_ {2}\right), where x_ {1} and x_ {2} are the solutions of

Writing Equations Of Perpendicular Lines Analytic Geometry Video Khan Academy

Writing Equations Of Perpendicular Lines Analytic Geometry Video Khan Academy

− − 19 10 13 10 1 2 8 2 15 4 6 5 2 1 2 1 4 2 3 (iii) det(A) = 2 − (−10) = 12, det(B) = 8 − 3 = 5 Since neither is zero, as a result, they are both invertible matrices (iv) A−1 = − = − = − − − 5/ 12 1/ 12 1/6 1/6 5 1 2 2 12 1 5 1 2 2 2 ( 10) 1A b = − 1 a b = 6 (− 1) = − 6 Since ab is negative, a and b have the opposite signs Since ab is negative, the negative number has greater absolute value than the positive List all such integer pairs that give product 6 Since a b is negative, a and b have the opposite signsThe sum of all x ∈ 0, π which satisfy the equation s i n x 2 1 c o s x = s i n 2 (x 4 π ) is View solution Show that a sin 2 1 A sin 2 1 ( B − C ) b sin 2 1 B sin 2 1 ( C − A ) c sin 2 1 C sin 2 1 ( A −

What Is The Next Number In This Series 1 2 6 24 1 7 Quora

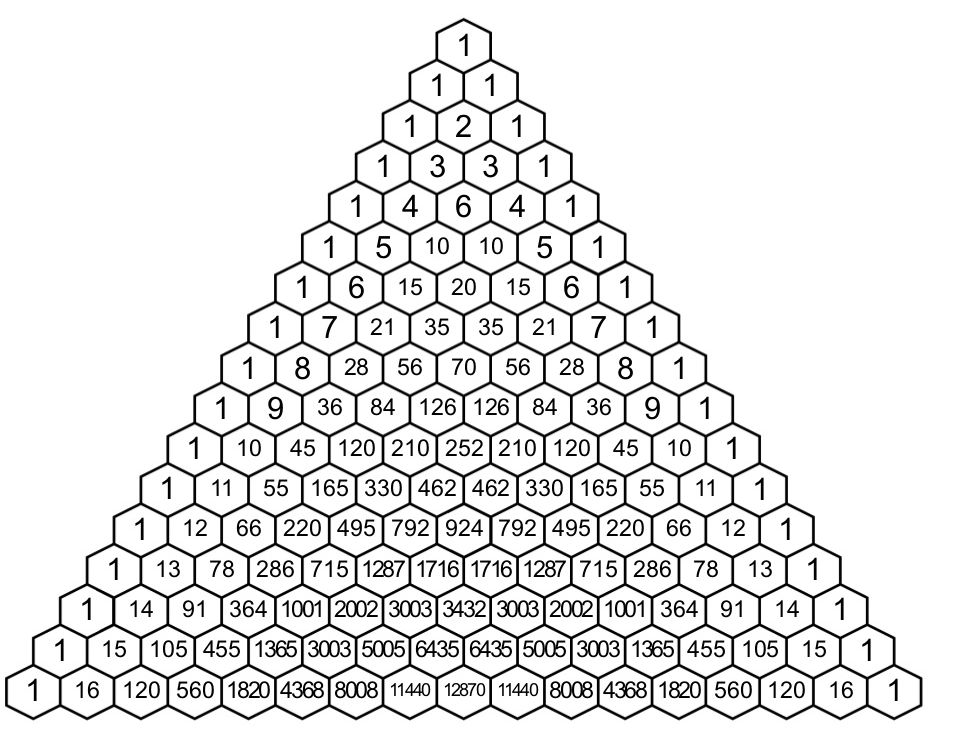
How Do You Use Pascals Triangle To Expand 2x 6 7 Socratic

( x − a) 2 f ( 3) ( a) 3!In the standard (x,y) coordinate plane, what is the midpoint of the line segment that has endpoints (3,8) and (1,−4) ? Reading 1 Jer 2316 Woe to the shepherds who mislead and scatter the flock of my pasture, says the LORD Therefore, thus says the LORD, the God of Israel, against the shepherds who shepherd my people You have scattered my sheep

Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples

Example 16 Solve 6x 1 3 X 3 6 Chapter 2 Class 8 Teachoo

( x − a) f ′ ′ ( a) 2!在考虑一般级数1 − 2x 3x 2 − 4x 3 5x 4 − 6x 5 后这个概念变得更明晰了。 这个一般级数是由表达式 1 ⁄ (1 x ) 2 展开而成，当我们让 x = 1 后，这个级数就确确实实地相等了。( x − a) 3 ⋯ (x−a)3 ⋯ Taylor series are extremely powerful tools for approximating functions that can be difficult to compute otherwise, as well as evaluating infinite sums and integrals by recognizing Taylor

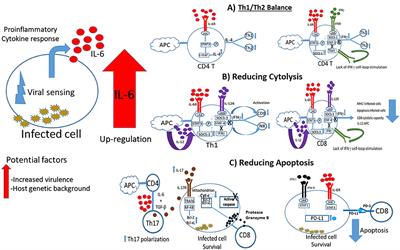
Frontiers The Role Of Interleukin 6 During Viral Infections Microbiology

Trapezoidal Rule

The lowly will hear me and be glad R Taste and see the goodness of the Lord Glorify the LORD with me, let us together extol his nameDenotes the factorial notationHis praise shall be ever in my mouth Let my soul glory in the LORD;

Warm Up Simplify 2 1 4 4 6 Solve For X 2 Ppt Download

A Graph Passes Through The Points 1 6 3 13 5 Chegg Com

A (−2,−12) B (−1,−6) C (11/2 ,3/2) D ( 2, 2) E (4,−12) 473 views Share Follow2 0 1 6!Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Exercise 1 2 Cramer S Rule Problem Questions With Answer Solution

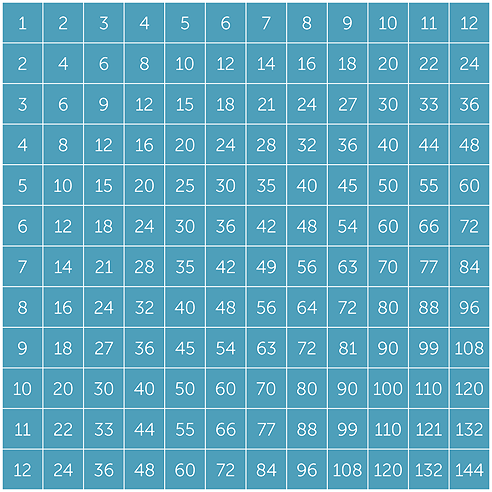
Multiples Factors And Powers

Solve linear equations using a general strategy Step 1 Simplify each side of the equation as much as possible Use the Distributive Property to remove any parentheses Combine like terms Step 2 Collect all the variable terms on one side of the equation Use the Addition or Subtraction Property of Equality Step 3Now −𝑡𝑎𝑛1(tan 7𝜋 6) = tan−1(tan𝜋 6) = 𝜋 6 ∈ (π/2, π/2) As tan1 tan(x) = x if x ∈ (π/2, π/2) So the value of 𝑡𝑎𝑛−1(tan 7𝜋 6) is 𝜋 6 3 Prove that 𝐢 − = 𝐚 Solution Step 1 Find the value of cos x and tan x Let us consider sin−13 5 = , then sin x = 3/5 So, cos x = √1−sin2 = √1For example, L(1,−1) = (1,−2,−1) and L(2,6) = (2,4,6) This particular function satisfies the linearity condition below, and so would be called a linear transformation from R2 to R3 Definition 31 Let Vand Wbe two vector spaces Let Lbe a function defined

Find The Determinant Of 6 3 3 3 6 1 1 1 6 Gauthmath

Midpoint Formula Analytic Geometry Article Khan Academy

Is divided by 19? Figure 613 The area bounded by the functions f(x) = (x − 1)2 1 and g(x) = x 2 on the interval 0,3 The area between the two curves on 0, 3 is thus approximated by the Riemann sum A ≈ n ∑ i = 1(g(xi) − f(xi))Δx, and then as we let n → ∞, it follows that the area is given by the single definite integral33 an − 7an − 2 an − 5 = 0 Ans Yes 34 an an − 1 = 1 Ans No 35 A vending machine dispensing books of stamps accepts only $1 coins, $1 bills, and $2 bills Let an denote the number of ways of depositing n dollars in the vending machine, where the order in which the coins and bills are deposited matters

Finding The Slope Of A Line

U1a L1 Examples Factoring Review Examples Ppt Video Online Download

SECTION 71 INTEGRATION BY PARTS ¤ 5 30 Let =arctan(1 ), = ⇒ = 1 1(1 )2 −1 2 − 2 1, = By(6), √ 3 1 arctan 1 = arctanWhere f (2k−1) is the (2k − 1)th derivative of f and B 2k is the 2kth Bernoulli number B 2 = 1 / 6, B 4 = − 1 / 30, and so on Setting f(x) = x, the first derivative of f is 1The graph is situated with positive integers to the right and negative integers to the left In mathematics, 1 − 2 3 − 4 ···is an infinite serieswhose terms are the successive positive integers, given alternating signs ∑n=1mn(−1)n−1{\displaystyle \sum _{n=1}^{m}n(1)^{n1}}

Graphing Parabolas

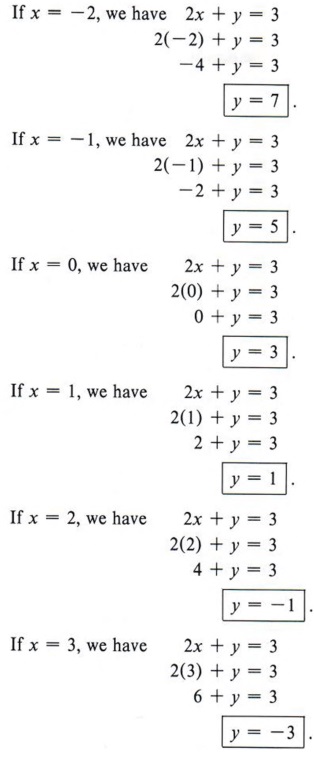
Graph Graph Inequalities With Step By Step Math Problem Solver

(M/J 13) 24 Discuss the nature of the following quadratic form 3x 1 2 3x 2 25x 3Question 1) If f(x, y) = 49 − 7x2 − y2, find fx(1, −6) and fy(1, −6) and interpret these numbers as slopes fx(1, −6) = fy(1, −6) = 2) Find the first partial derivatives of the function f(x, y) = x8 3xy7 fx(x, y) = fy(x, y) = 3) Find the first partial derivatives ofLet A= 3725 and B= 6879 verify thatAB−1=B−1A−1 Give Let A=3 7 2 5 and B=6 8 7 9 verify that (AB)−1 = B−1A−1 Please scroll down to see the correct answer and solution guide

1

Solve Solve Inequalities With Step By Step Math Problem Solver

)−3 12 = 2 5 ×(−61 14)−1 4 = 2 5 ×(−61 14)−1 4 (by distributivity) = 2 5 ×(−5 14)−1 4 = 2 5 ×(−5 14)−1 4 = (−10 70)−1 4 = −1 7 −1 4 = −4−7 28 = −11 28 2 Write the additive inverse of each of the following (i) (ii) − (iii) − − (iv) − (v) − Solution (i) 2 8 Additive inverse of 2 8 is −2 8 (iiIαt, where i and α are constants, i= −1 6 – 8 Each function F(s) below is defined by a definite integral Without integrating, find an explicit expression for each F(s) Hint each expression is the Laplace transform of a certain function Use

What Is 2 10 1 6

Lego Tile 1 X 2 X 5 6 With Stud Hole In End With Black Pattern Hyphen Minus Sign Brick Owl Lego Marketplace

Integers

Equation Calculator Symbolab

Divisibility Rule Wikipedia

Translations

Distance Formula Calculator Step By Step Examples Tutors Com

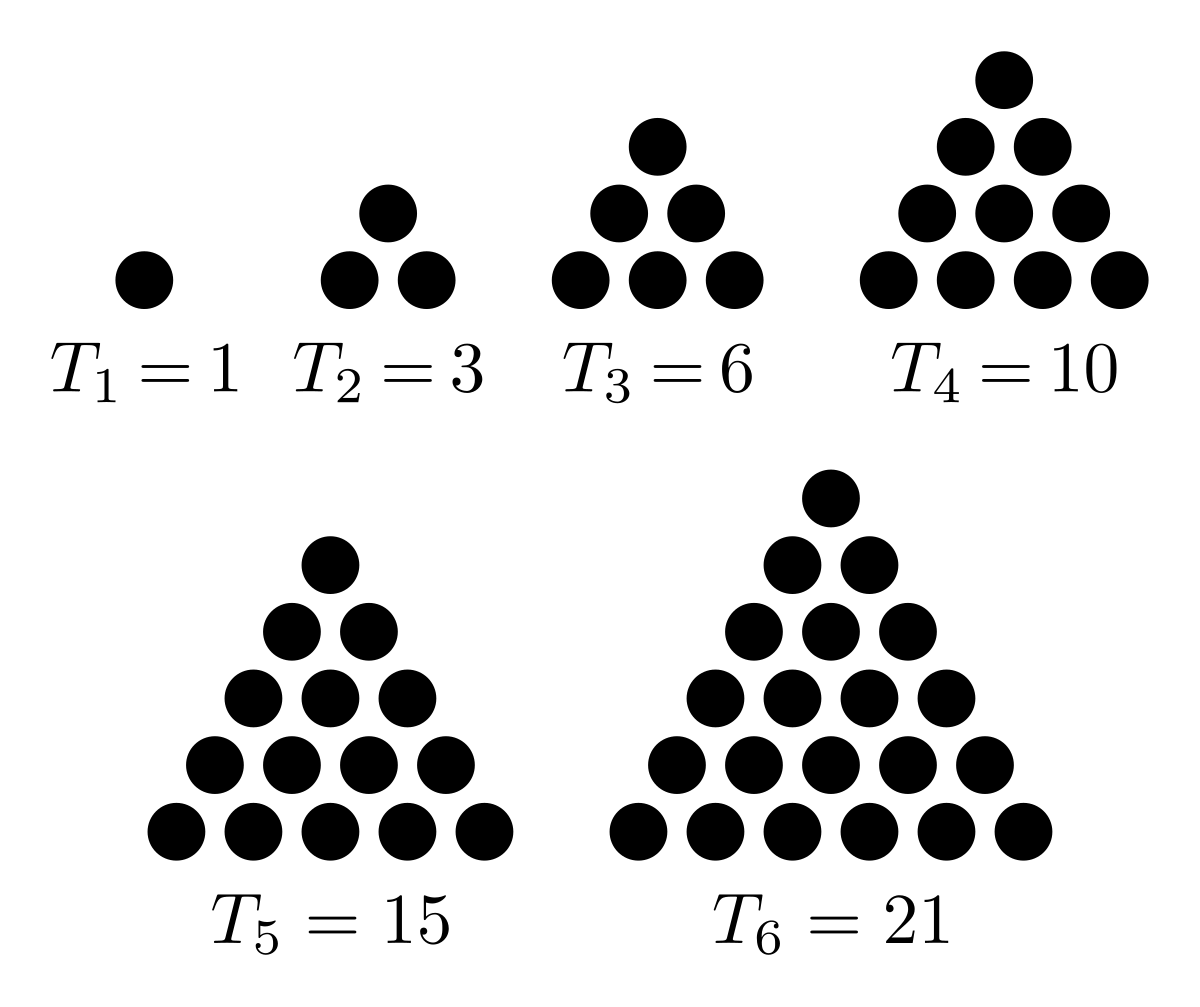
Triangular Number Wikipedia

Rd Sharma Solutions For Class 7 Maths Chapter 7 Algebraic Expressions Download Free Pdf

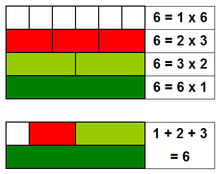
Perfect Number Wikipedia

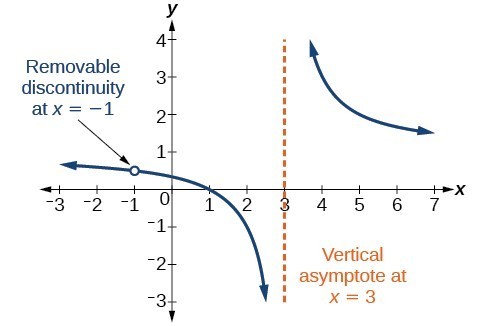
Identify Vertical And Horizontal Asymptotes College Algebra

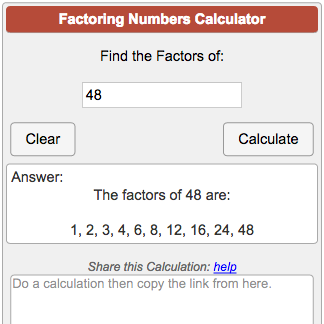
Factoring Calculator

6 Ways To Find The Domain Of A Function Wikihow

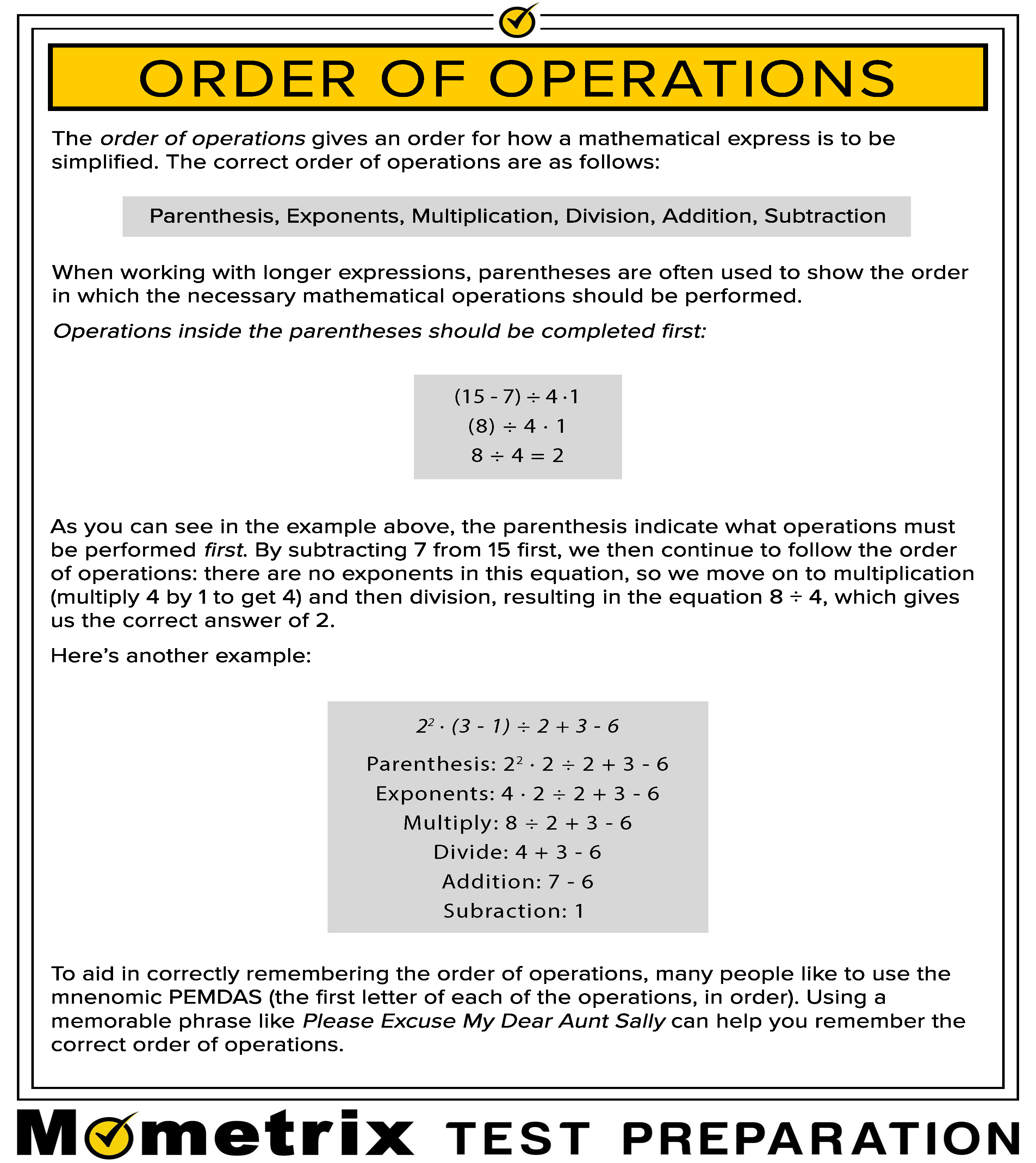
What Are The Order Of Operations Video Practice

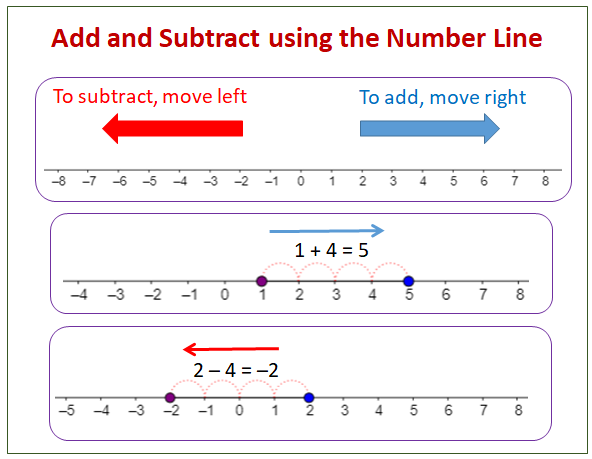
Subtracting Integers Using The Number Line Solutions Examples Worksheets Videos Games Activities

Perfect Number Wikipedia

Problem 3 33 A Manager Uses This Equation To Predict Chegg Com

Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1

Ex 6 1 16 Solve 2x 1 3 3x 2 4 2 X 5

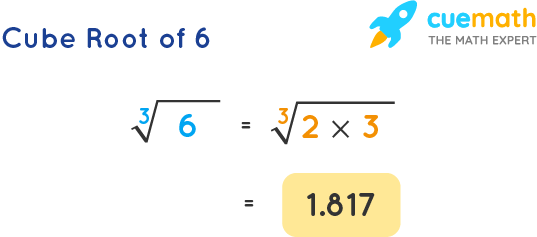
Cube Root Of 6 How To Find The Cube Root Of 6 Solved

1

How To Find The General Term Of Sequences Owlcation

Http College Cengage Com Mathematics Hubbard Discovery Visualization 3e Students Downloads Ti Keystrokes Pdf

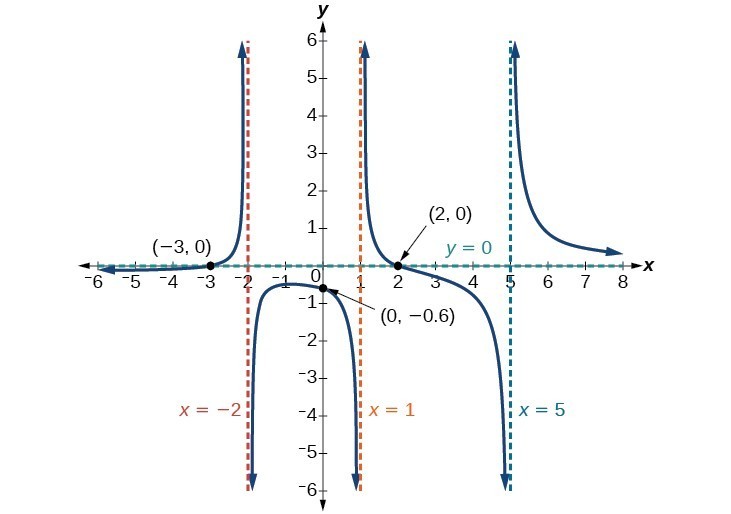
Identify Horizontal Asymptotes College Algebra

1 2 3 4 Wikipedia

Trapezoidal Rule

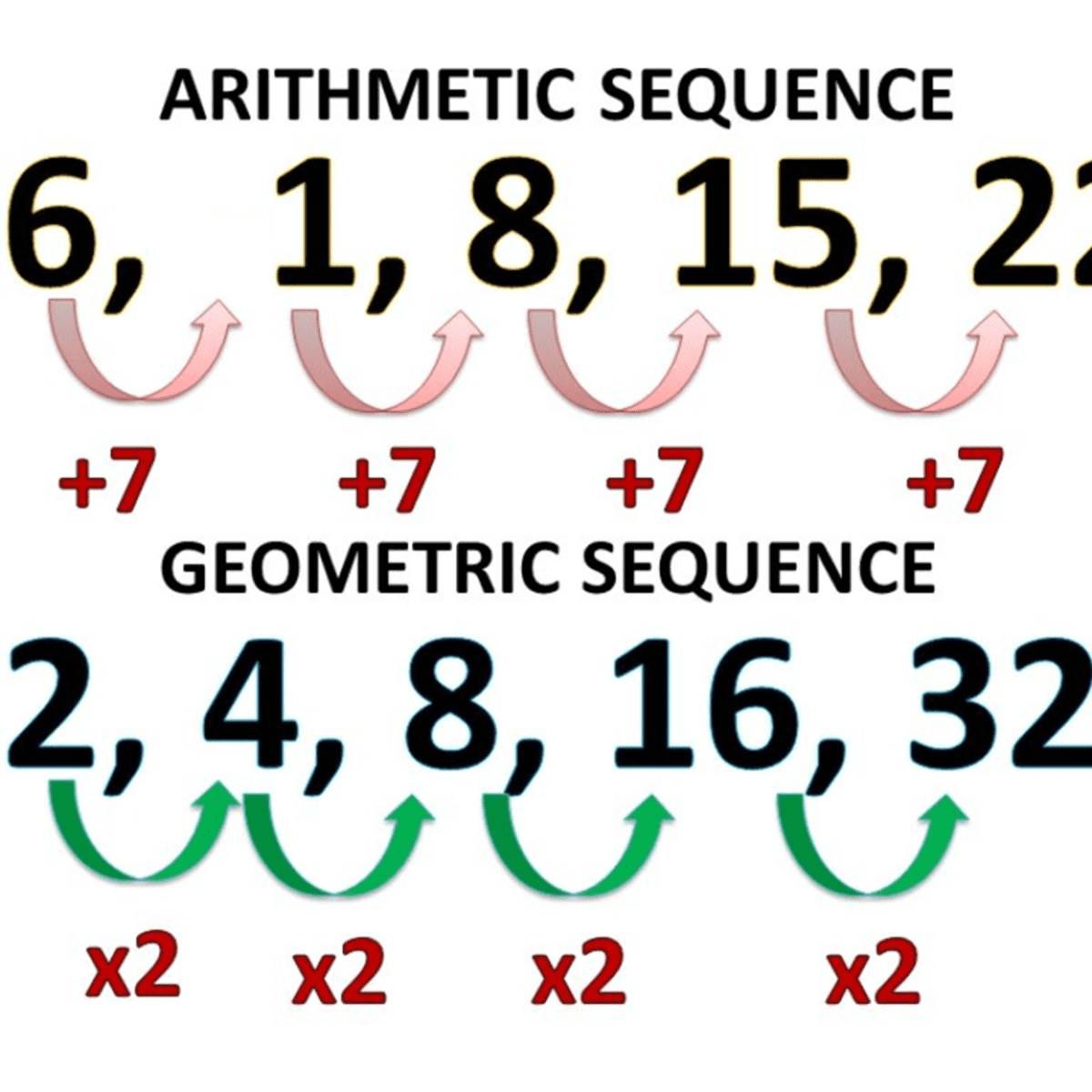
How To Find The General Term Of Sequences Owlcation

Finding The Slope Of A Line

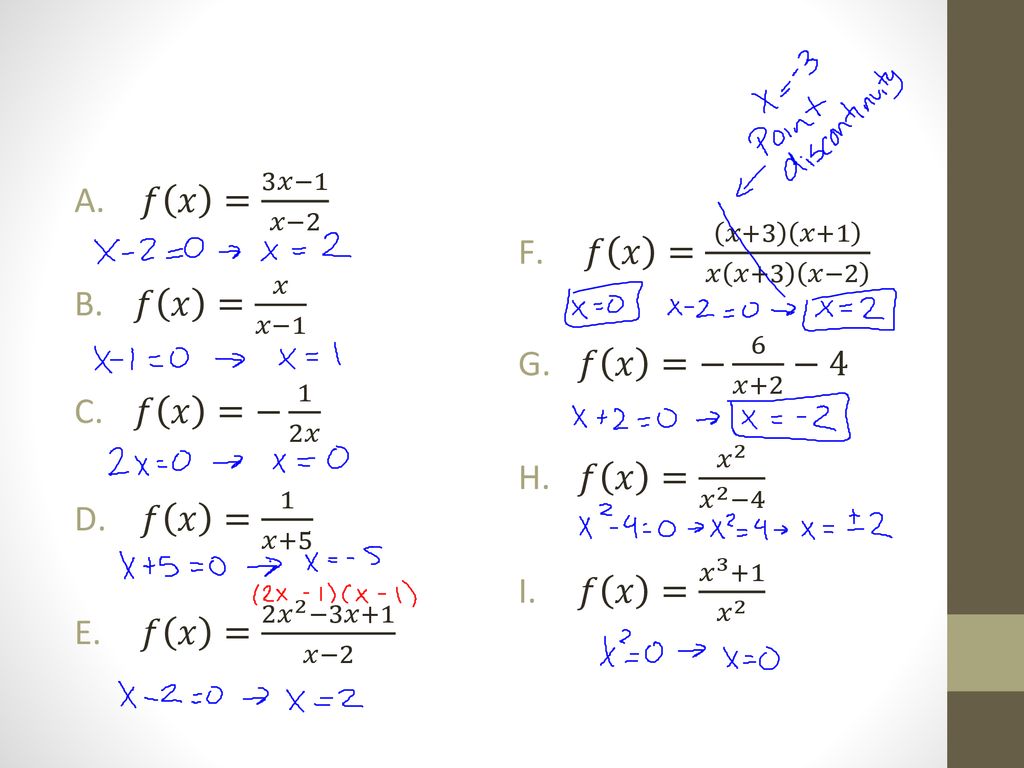
3 7 Graph Of Rational Functions Ppt Download

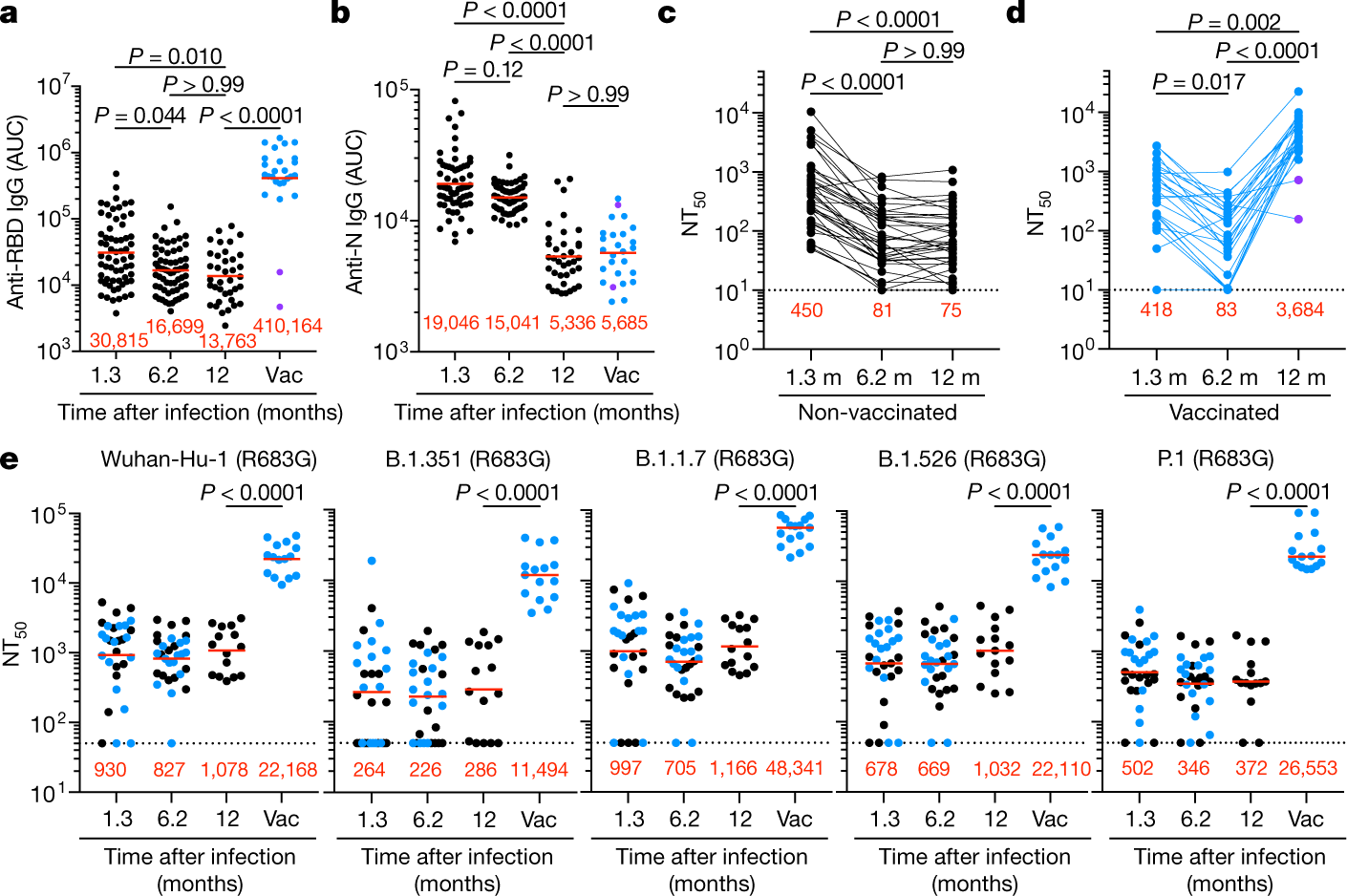
Naturally Enhanced Neutralizing Breadth Against Sars Cov 2 One Year After Infection Nature

The Factorial In Mathematics And Statistics

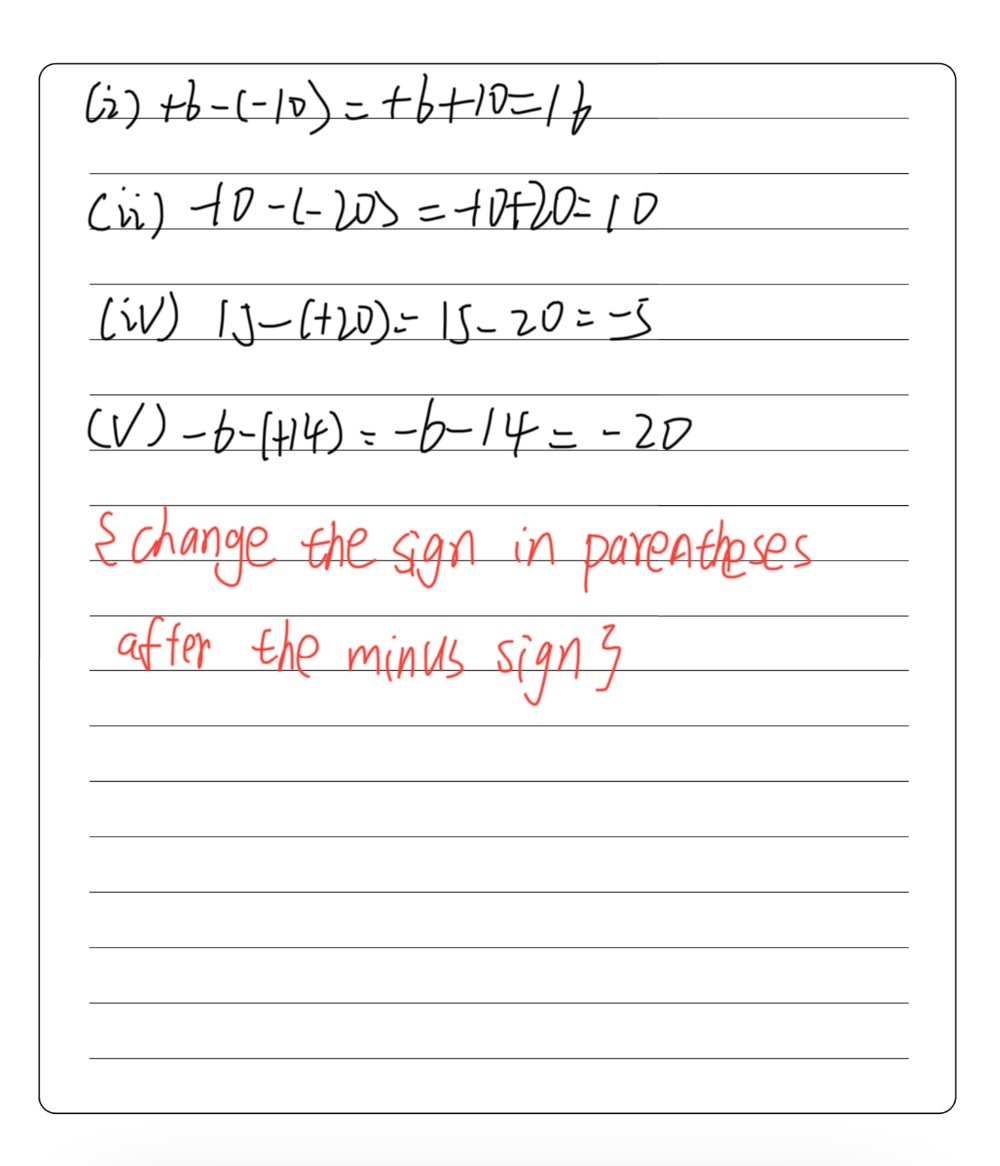
2 Subtract I 6 From 10 Ii 10 Gauthmath

What Is The Expansion Of Log 1 X Quora

6 Ways To Find The Domain Of A Function Wikihow

What Is 1 6 1 10

1

Solve Solve Inequalities With Step By Step Math Problem Solver

Math Temple Edu Ugrad New Students Placement Preparation Math 1021 Beginning Of Semester Review Pdf

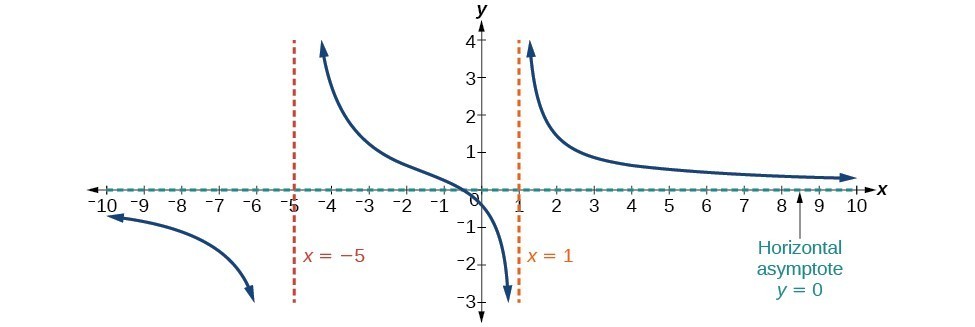
Identify Horizontal Asymptotes College Algebra

Divisibility Rules How To Test If A Number Is Divisible By 2 3 4 5 6 8 9 Or 10 Divisibility Calculator

1

Ex 11 5 1 State Which Are Equations With A Variable A 17

Rd Sharma Solutions For Class 8 Chapter 1 Rational Numbers Download Free Pdf

7th Grade Math Activities And Games Sadlier School

Natural Variation Identifies Sni1 The Smc5 6 Component As A Modifier Of Meiotic Crossover In Arabidopsis Pnas

Graphing Parabolas

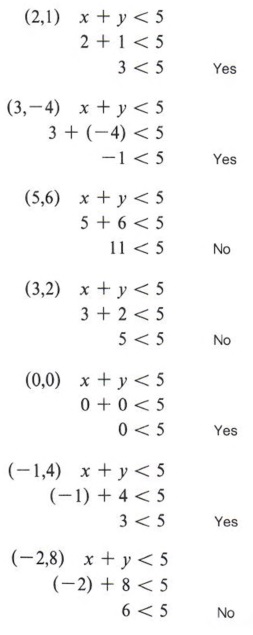
Graph Graph Inequalities With Step By Step Math Problem Solver

Graph Graph Inequalities With Step By Step Math Problem Solver

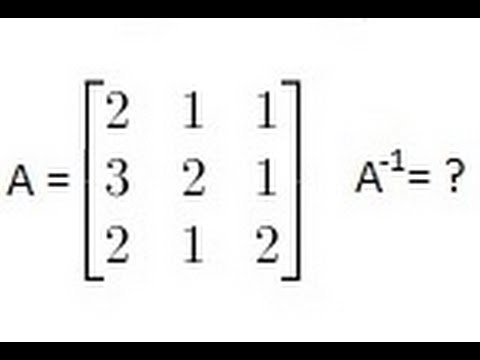
Algebra Finding The Inverse Of A Matrix 1 Of 2 A 3x3 Matrix Youtube

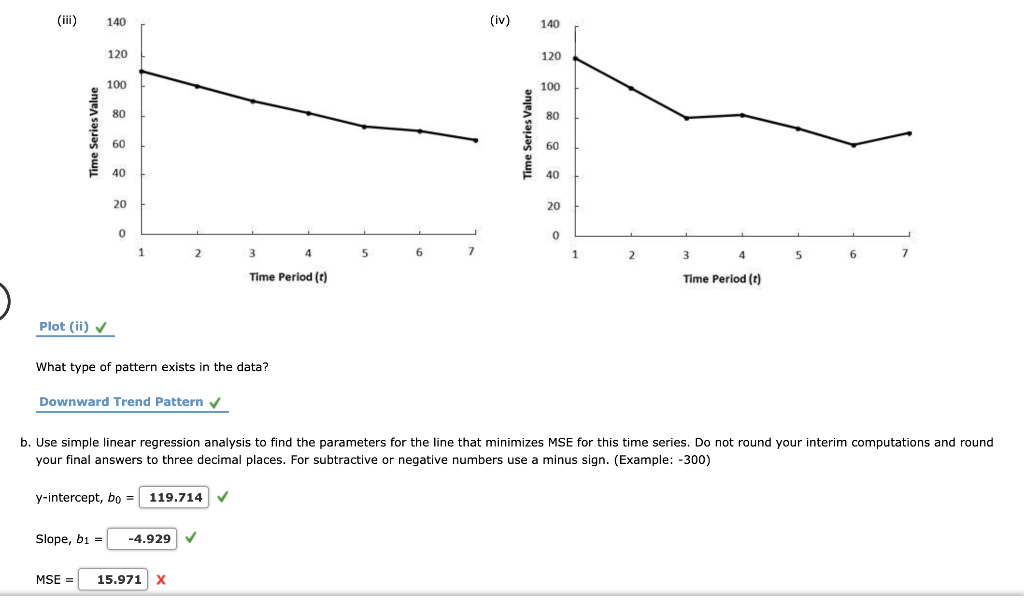
Problem 6 19 Consider The Following Time Series T 1 Chegg Com

Www Westada Org Cms Lib Id Centricity Domain 4941 2 5 key 3 Pdf

Unit 4 Day Ppt Download

Exercise And Cardiovascular Health Circulation

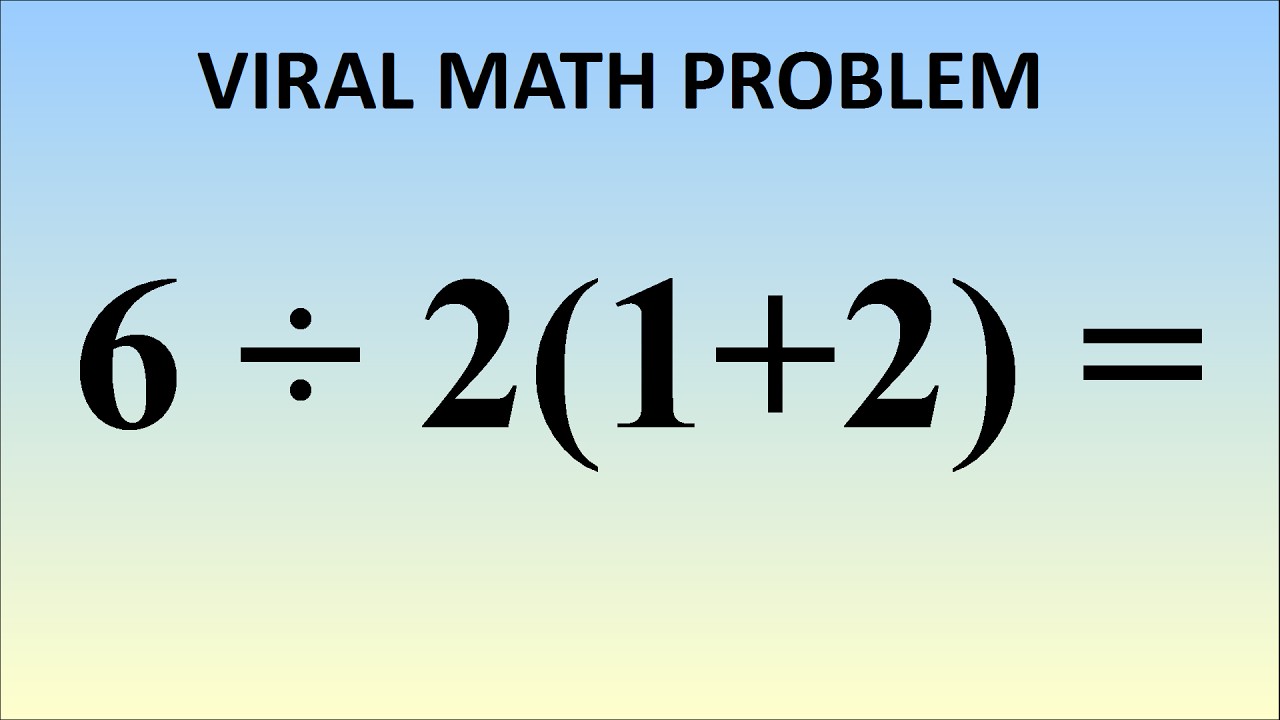
What Is 6 2 1 2 The Correct Answer Explained Mind Your Decisions

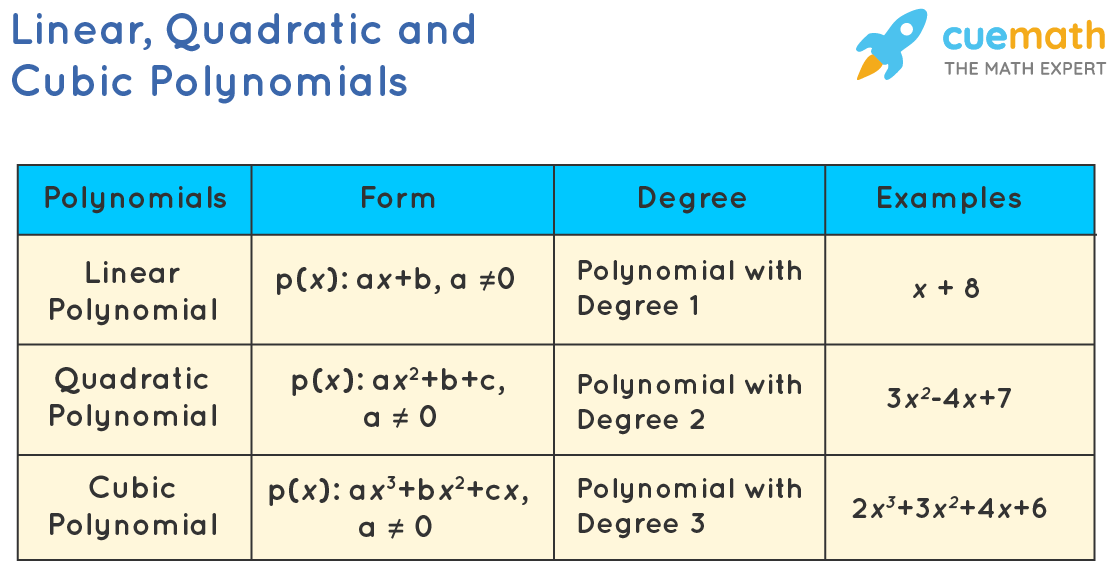
Linear Quadratic Cubic Polynomials Examples Classification

Example 1 Find 3 7 6 11 8 21 5 22 Chapter 1 Class 8

Binary Operation Introduction Properties Types With Solved Examples

Free Worksheets For Linear Equations Grades 6 9 Pre Algebra Algebra 1

How To Find The General Term Of Sequences Owlcation

Problem 7 07 Algorithmic The Following Questions Chegg Com

The Midpoint Formula Purplemath

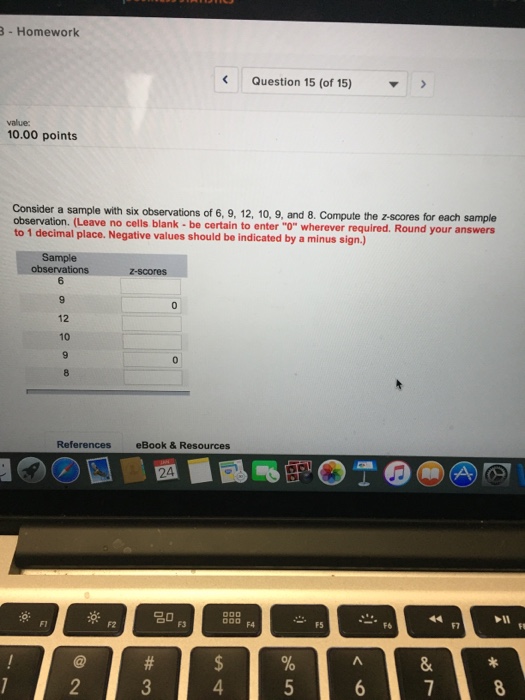
Consider A Sample With Six Observations Of 6 9 12 Chegg Com

Bell Work Week 21 Pick A Math Word And Write The Definition Chapter 6 Ppt Download

Interleukin 6 Receptor Antagonists In Critically Ill Patients With Covid 19 Nejm

Simplifying An Expression With A Fraction Bar Prealgebra

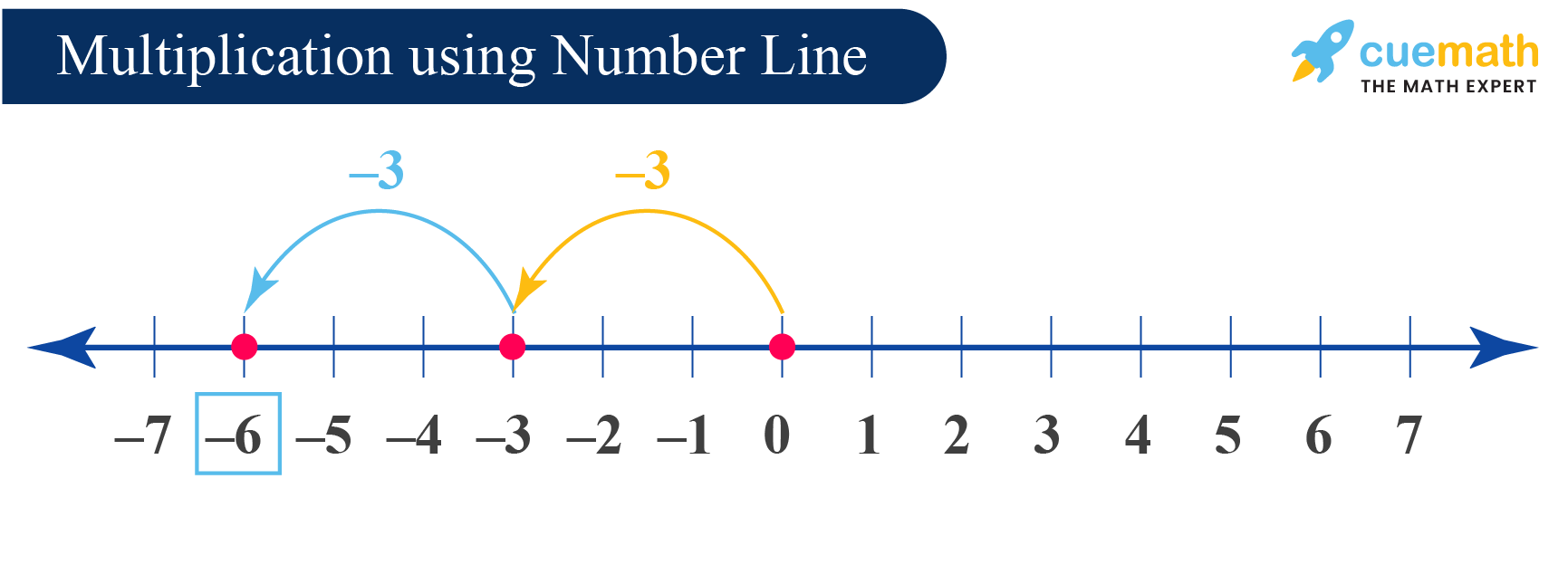
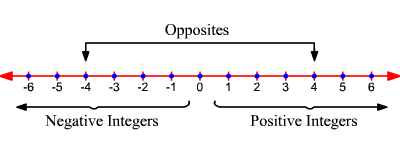
Integers Definition Properties Examples Of Integers

What Is An Integer Definition Examples Video

Graphing Parabolas

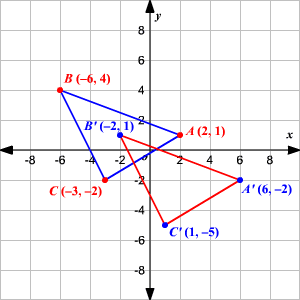
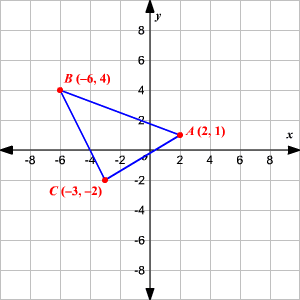
Translations

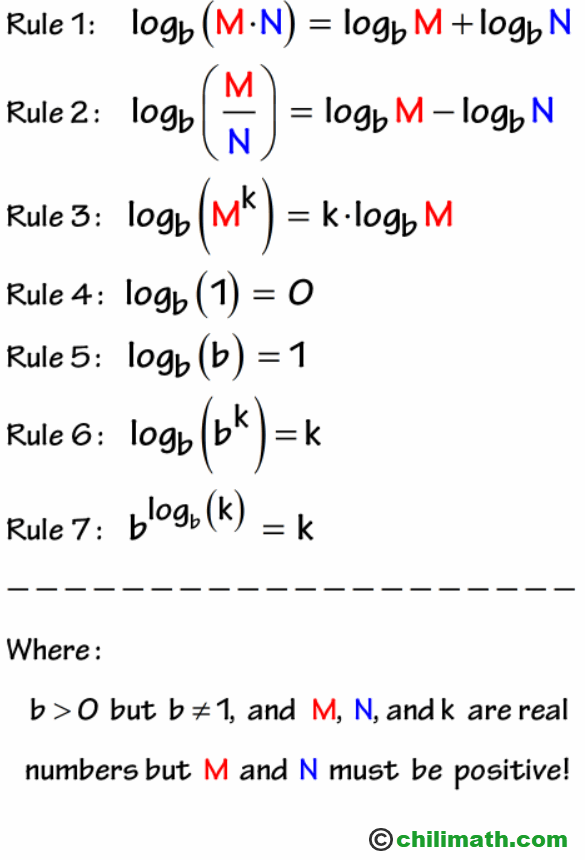
Logarithm Rules Chilimath

Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples

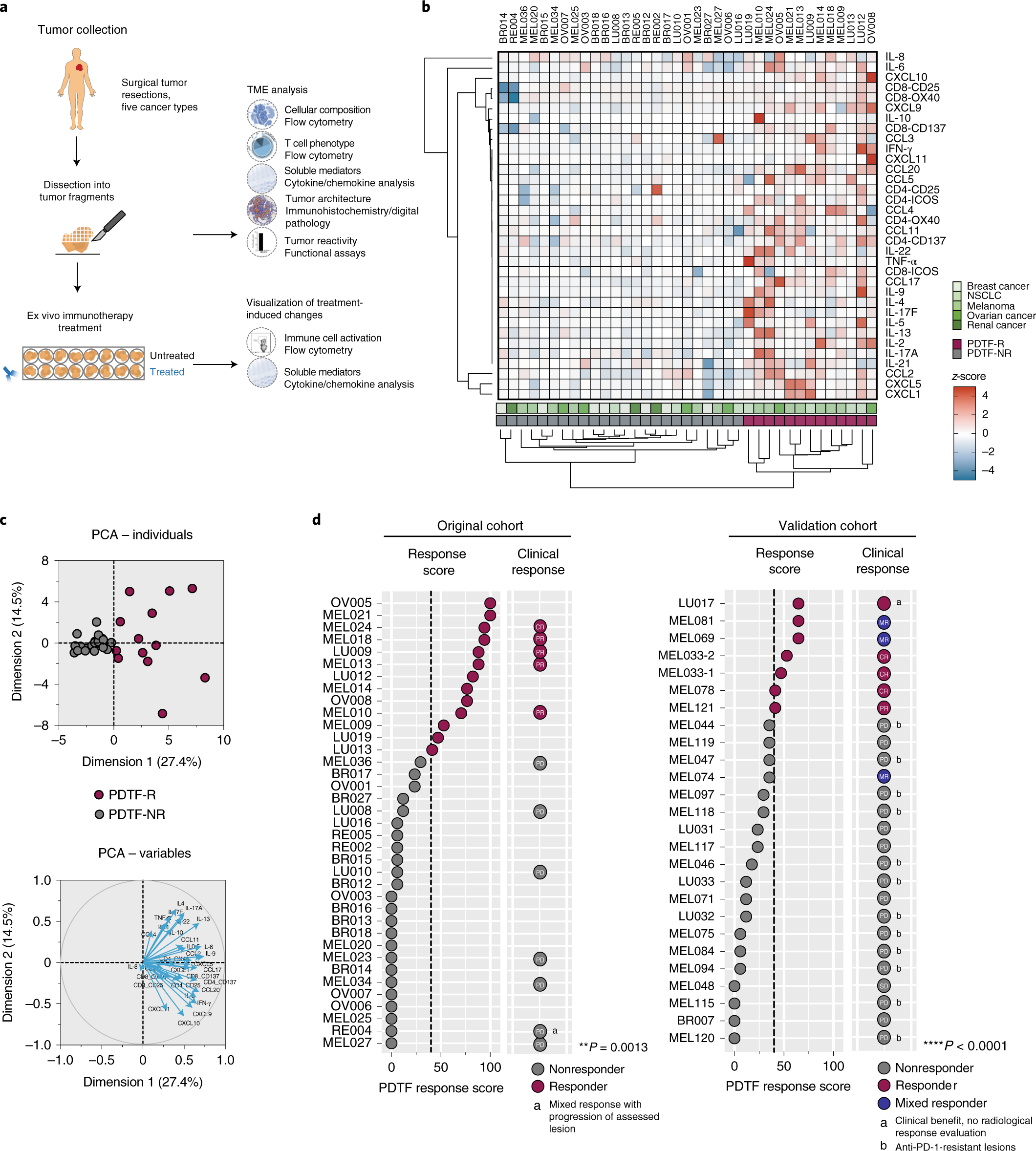
An Ex Vivo Tumor Fragment Platform To Dissect Response To Pd 1 Blockade In Cancer Nature Medicine