定理の内容はやや難しいですが,定理名は非常に印象的です。 円に内接する多角形を三角形分割して,その三角形たちの内接円の半径の和 r r r を計算する。 r r r 三角関数の公式は加法定理から 今回からいよいよ三角関数における重要な 「公式」 に触れていきます。 ですが、新しい「公式」は 常に今までの知識を活用して作られます し、その 今までの知識だけでは解けなくなった問題を解くために作ったり、考えたりする ものです。図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し
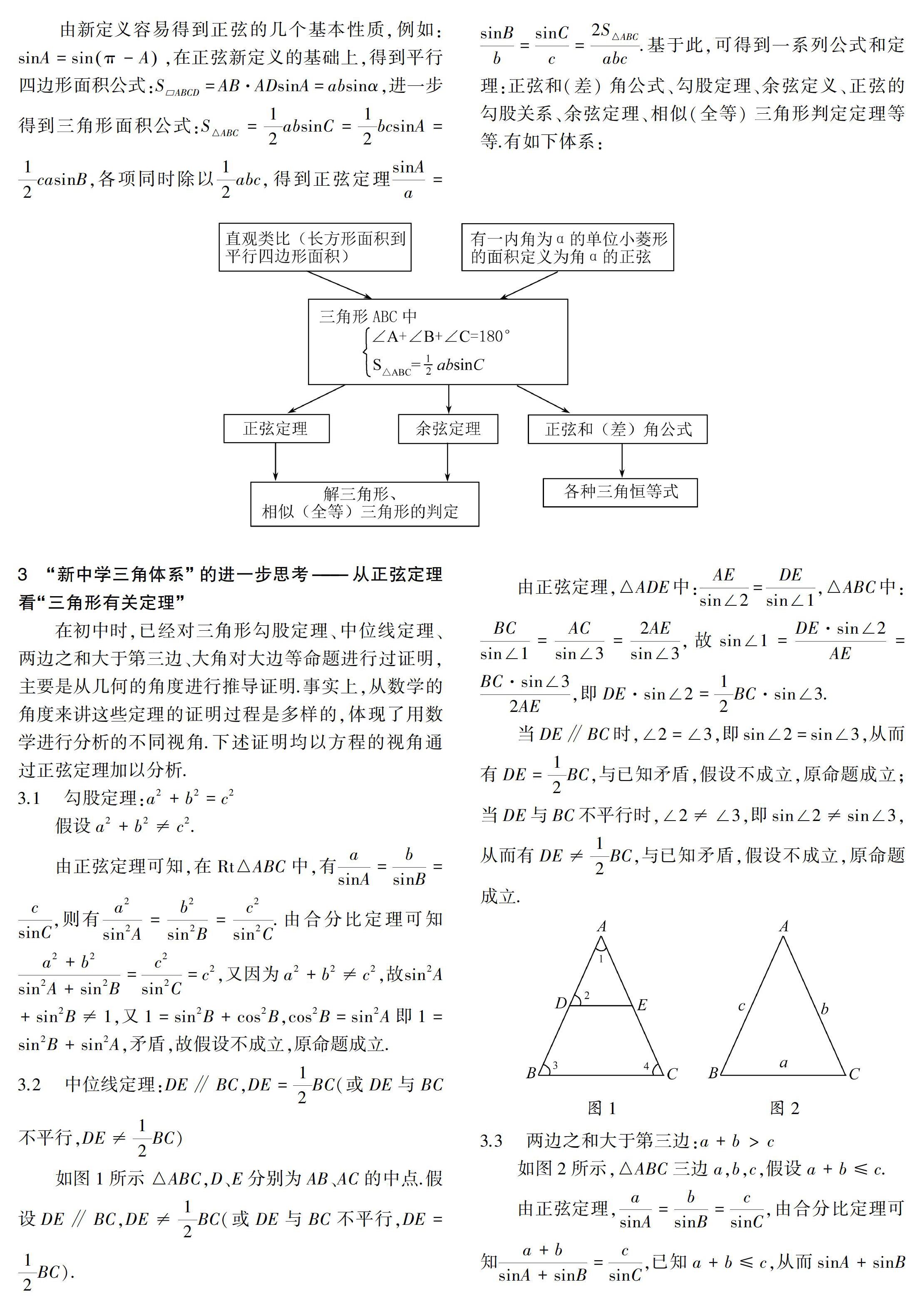
新中学三角体系 概述及其进一步思考 参考网
三角定理 证明
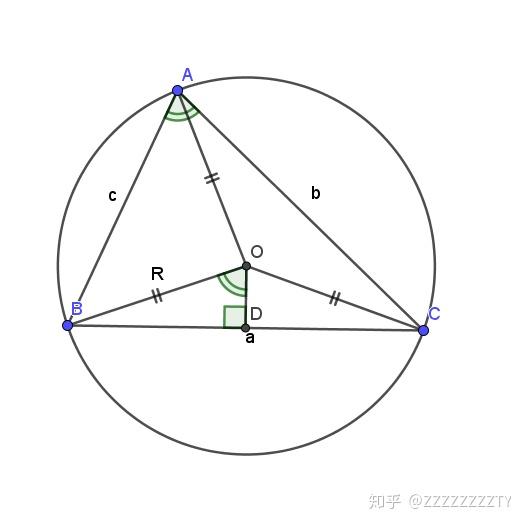
三角定理 证明- 1、正弦定理 如上图所示,a,b,c为圆上三点,则有: 2、球面三角正弦定理 如上图红色弧线所示,球面三点a,b,c构成球面三角形,球面角分别为 , , (球面角其实基于二面角定义,例如,球面角 等于二面角c~oa~b); 则有:定理一覧 円を含む図形 方べきの定理 トレミーの定理 シムソンの定理 シュタイナーの定理 アルハゼンの定理 ニュートンの定理 九点円の定理 フォイエルバッハの定理 ターレスの定理 パスカルの定理 アポロニウスの定理 ブリアンショの定理



正余弦定理 万图壁纸网
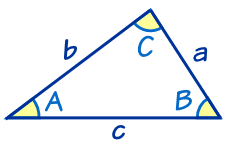
三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ: =,() = / /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる:要证明这个定理,画线段bf 平行于 ae 来形成平行四边形bcef: 三角形 abc 和 bdf 有相等的角,所以是相似三角形(为什么?去相似三角形的判定看 aa 的部分。) 边ab 对应边bd,边ac 对应边bf。 所以 ab/bd = ac/bf;余弦定理 三角形の各辺 a , b , c と各角 A , B , C の間には以下に示す関係がある. a 2 = b 2 c 2 − 2 b c cos A b 2 = c 2 a 2 − 2 c a cos B c 2 = a 2 b 2 − 2 a b cos C
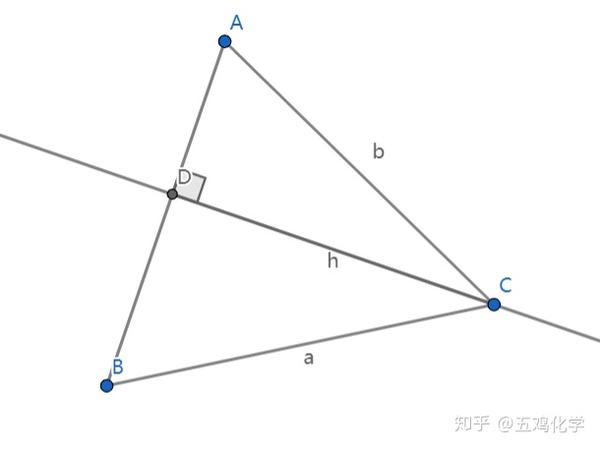
正弦定理の導出 前半 \begin {equation} \frac {a} {\sin A}=\frac {b} {\sin B}=\frac {c} {\sin C} を導出してみましょう。 \end {equation} \\ まずは下図のような三角形を考えます。 この上図の三角形より AD の辺の長さを求めます。 ABDにおいて \\ \begin {eqnarray} AD &=& AB\sin B正弦定理(The Law of Sines)是三角学中的一个基本定理,它指出"在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆半径的2倍",即a/sinA = b/sinB =c/sinC = 2r=D(r为外接圆半径,D为直径)。 正弦定理的公式: 在任意 ABC中,角A、B、C所对的 中線定理とは まずは中線定理について知りましょう。 中線定理は、三角形の中線の長さと辺の長さの関係を表す定理 であり、パップスの定理とも知られています。 次の三角形をみてくだ
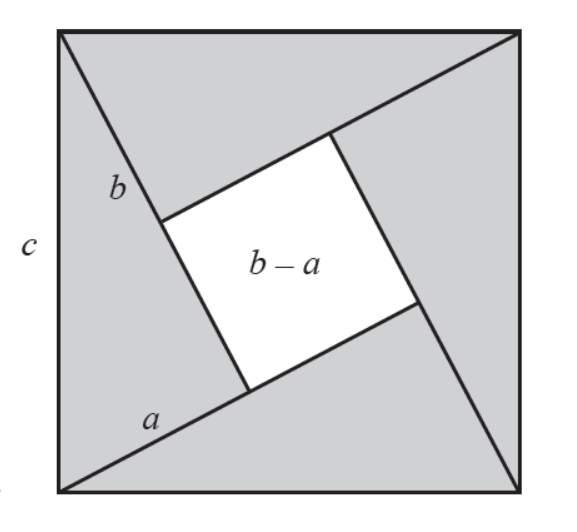
== 《三平方の定理》 == → 印刷用pdf版は別頁 1番目の三角形として直角をはさむ2辺の長さが1,1である直角三角形を作ります.1、正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,即在 abc中, (其中r为 abc外接圆的半径) 上式对任意三角形均成立 正弦定理可以变形为:① ;② , , ;③ , , ;④ , , 等形式,以解决不同的三角形问题 2、三角形中正弦定理的应用 全等三角形定理 天奇生活 字体: 大 中 小 1、三组对应边分别相等的两个三角形全等;2、有两边及其夹角对应相等的两个三角形全等;3、有两角及其夹边对应相等的两个三角形全等;4、有两角及其一角的对边对应相等的两个三角形全等;5



三角形的正弦定理 余弦定理 初中数学 学习资料大全 免费学习资源下载



三角定理讲课视频 西瓜视频搜索
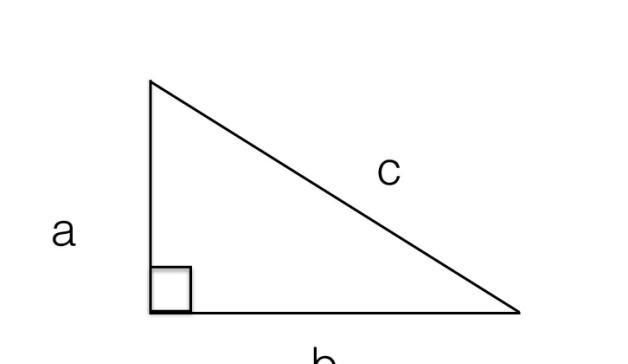
而且 bf = ce; ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c²三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。




余弦三角数学定律浮动三角形png图片素材免费下载 图片编号187 Png素材网



正余弦定理 万图壁纸网
「定理」とよばれている代表的なものは「円周角の定理」,「三平方の定理」です。 例として「二等辺三角形」で説明してみましょう。 定義二辺が等しい三角形 (図の三角形abcでab=ac) 三角函數 (英語: Trigonometric functions )是 數學 中常見的一類關於 角度 的 函數 。 三角函數將 直角三角形 的內角和它的兩個邊的 比值 相關聯,也可以等價地用與 單位圓 有關的各種線段4 三角形の角と辺 ppooiinntt ama05 3 三平方の定理の応用(高校内容) c ab b a c c a b m ここでは,三平方の定理を利用して,三角形の辺の間に成り立つ関係について学習してみましょう。



1 1 4 锐角三角函数与射影定理 人教版高中选修 B版 4 1数学电子课本 数九网



正弦定理 余弦定理 玄数
三角関数の加法定理 sin(α ± β) = sinαcosβ ± cosαsinβ cos(α ± β) = cosαcosβ ∓ sinαsinβ tan(α ± β) = tanα ± tanβ 1 ∓ tanαtanβ まずは,この定理が成り立つことを確かめたいと思います。 証明にはなりませんが,イメージをつかむために α , β , α β がいずれ このとき、円周角の定理より、∠apb=60°であることがわかります。 いま、 2pa=3pbになるときのpaの長さ を求めたいので、 2pa=3pb⇔papb=32より、x>0を満たすxをもちいて、 pa=3x pb=2x とおくことができます。 ここで、三角形apbに余弦定理を用いて、三角形の辺の長さや角の大きさを求めたいときは、正弦定理や余弦定理が有効ですが、その際、どちらを使えばよいのかは、確かに迷うところですね。 そこでまず、各々の定理について確認しておきましょう。 下の図のように3辺の長さが a , b , c で、辺に



1




高考数学考点之正 余弦定理及解三角形 王羽课堂
三角形の定理や性質 by omusoshiru 公開 19年7月12日 更新済み 19年7月10日 1三平方の定理(ピタゴラスの定理)→ 印刷用pdf版は別頁 三角関数の加法定理,倍角公式,3倍角公式,半角公式 三角関数の和や積には多くの公式がありますが,「加法定理は覚える,他は作る」というのが,作者おすすめの考え方です。・・・ただし,そういう公式があるということと,およその形は記憶にとどめます。検索語:三角比 三角関数の加法定理 三角比の三角形への応用 オイラー線の傾き 1 はじめに 高校数学「数学i」において三角比および三 角形などへの応用について学習する。応用の内 容は大体,正弦定理,余弦定理,三角形の解法,



勾股定理



由边的数量关系识别直角三角形 定理的应用 16 2由边的数量关系识别直角三角形 初中冀教版 数学中国网
通常的三角函数是在 平面直角坐标系 中定义的。 其 定义域 为整个 实数 域。このページでは,はじめに, sin (α β) , cos (α β) などの ( )をはずす公式「三角関数の加法定理」を解説し,その応用として「2倍角公式」「3倍角公式」「積和の公式」「和積の公式」を解説する. 三角関数の加法定理三平方の定理による辺の長さの計算です。三平方の定理は、 直角三角形の三辺をa,b,cとする。斜辺(最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。別名ピタゴラスの定理とも呼ばれます。 式は綺麗ですが、二乗が出てきます。



三角马登定理椭圆复数三角形中的steiner点png图片素材免费下载 图片编号 Png素材网




03勾股定理的逆定理勾股定理初中数学初二 Youtube
所以 ab/bd = ac/ce;




正弦定理 三角学中的基本定理 搜狗百科



全等三角形的性质定理 西瓜视频搜索




正余弦定理 揭示三角形边角关系的定理 搜狗百科



R Steriner定理的三角证法 科学猫




勾股定理應用2特殊直角三角形的勾股定理比例 Youtube
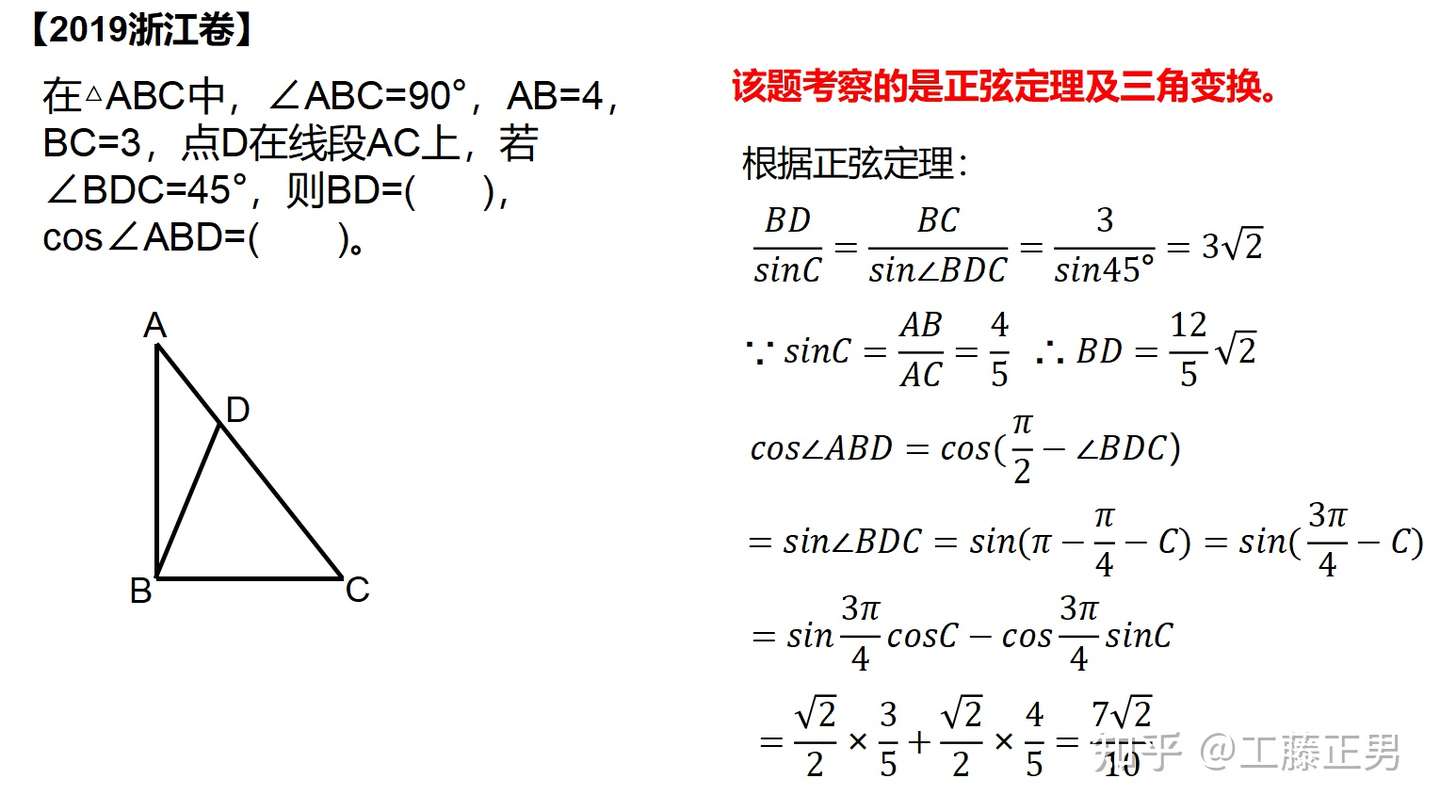



三角函数小题 解三角形专题 知乎
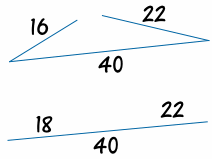



三角不等式定理
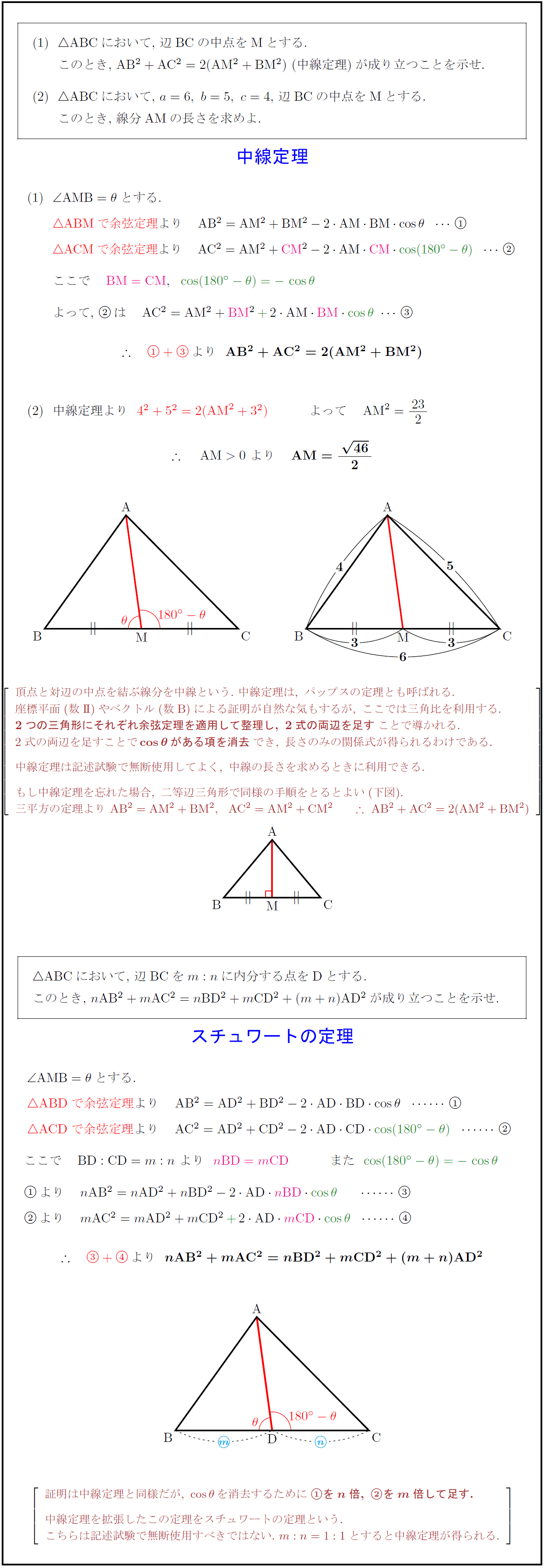



高校数学 中線定理 パップスの定理 とスチュワートの定理の三角比による証明 受験の月




数学干货丨高中数学正弦定理的五种证明方法 学霸讲解 提分必备 3326学习网




三角函数 正弦余弦定理及应用 羊羊的博客 Csdn博客 余弦定理



三角形勾股定理 如何学好三角函数和勾股定理 尚书坊



正弦定理 余弦定理 玄数



1




高考数学考点之正 余弦定理及解三角形 王羽课堂



人教版数学八年级下册勾股定理4 结合三角尺 腾讯视频



勾股定理为何能颠覆未来的 云世界 Hotpower的梦潭 与非博客 与非网



三角函数定理公式大全 初三网




畢氏定理x 圓x 三角學 余海峯david 物理喵phycat



勾股定理及勾股定理的逆定理 楠木轩




正 余弦定理在高考中的应用 参考网




寒假总动员 15年高三数学寒假作业专题07 三角函数在解三角形中的应用 背 下载 Word模板 爱问共享资料



悟空问答 关于勾股定理 有哪些有趣的题目 7个回答



勾股定理 锑星百科 Fandom




右三角形与勾股定理向量例证 插画包括有希腊语 蓝色 权利 正方形 欧几里德 镇痛药 例证




三角学 维基百科 自由的百科全书




正弦定理 教案1下载 Word模板 爱问共享资料




高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト




正弦与余弦定理 三角形与三角学 Mathigon




三角学 维基百科 自由的百科全书



少有人走的路 三角函数超入门 1 三平方定理的证明
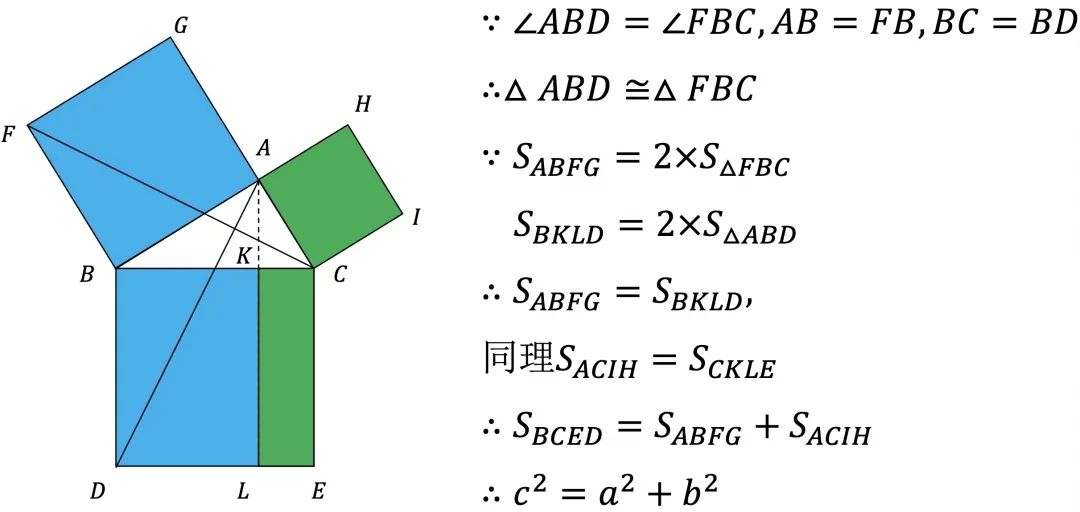



勾股定理竟然有500种证明方法 你会几种 小k算法 Csdn博客 勾股定理的500种证明方法




三角毕达哥拉斯定理正弦三角函数毕达哥拉斯三角恒等式 三角形png图片素材免费下载 图片编号 Png素材网




餘弦定理 维基百科 自由的百科全书



正弦定理和余弦定理 高中数学知识点 高考圈



必修五 高中数学必备知识点 3 解三角形之余弦定理



三角函数定义 初中三角函数公式及其定理 尚书坊




湘教版八年级初二数学下册 勾股定理三 课时作业word 牛图文
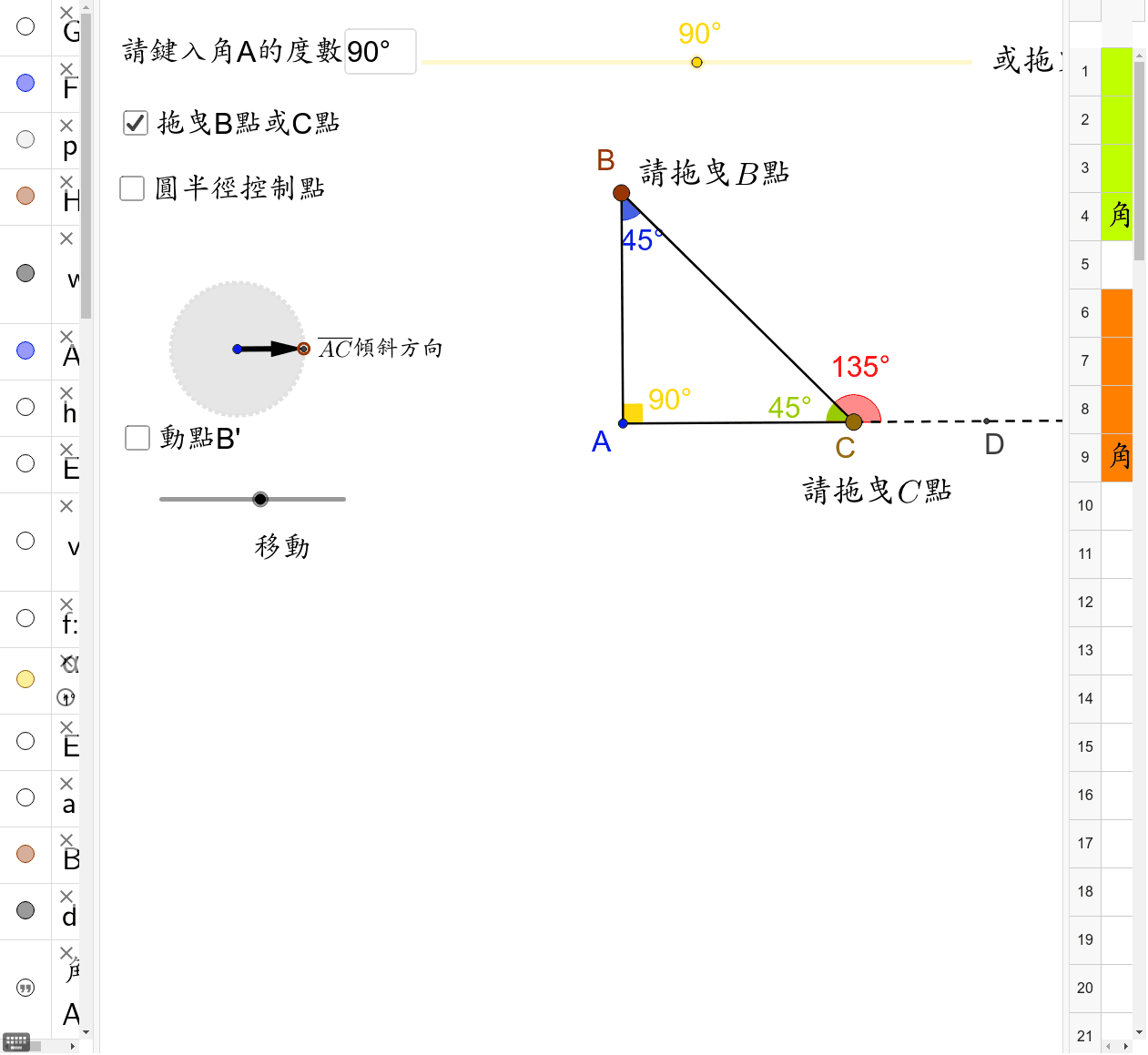



探索三角形外角定理 Geogebra
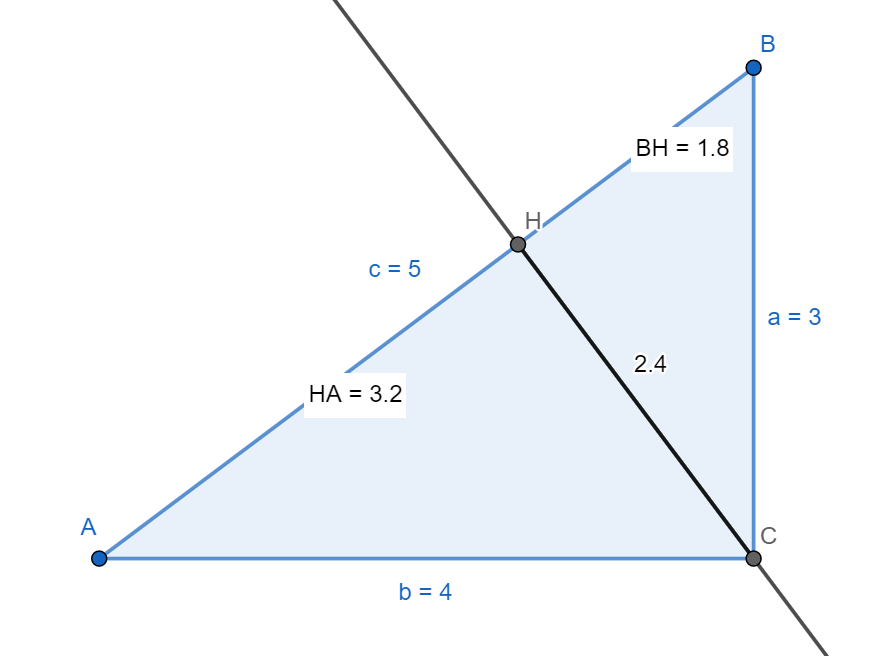



初中 彻底度量345三角形 345勾股数三角形的度数 人社网



用正弦定理确定三角形解的个数 哔哩哔哩 つロ干杯 Bilibili



必修五 高中数学必备知识点 3 解三角形之余弦定理
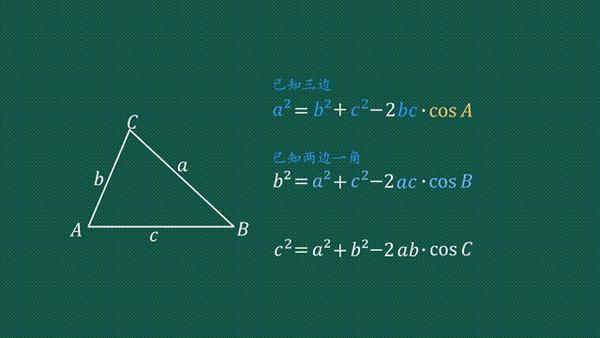



3分钟 搞懂余弦定理 知乎




初二暑假数学勾股定理单元练习30题 附答案 人人焦点




三角函数公式初中图解



三角函数 二 知乎




餘弦定理 维基百科 自由的百科全书




三角面积鹭公式毕达哥拉斯定理几何 三角形png图片素材免费下载 图片编号 Png素材网



中考學霸坦言 喫透勾股定理這些題型 幾何考試三角形從不丟分 雪花新闻




数学を愛する会 本発売 در توییتر 四平方の定理 三平方の定理の3次元版 直方体を斜めに切断してできた三角錐の表面積に関する等式



三角形的正弦定理 余弦定理 初中数学 学习资料大全 免费学习资源下载



余弦定理求三角形面积公式 高三网




三角函数勾股定理公式 勾股定理三角函数公式 三人行教育网 Www 3rxing Org




勾股定理库存图片 图片包括有数学 分度器 笔记本 黑板 课程 知识 代数 白垩 几何



1
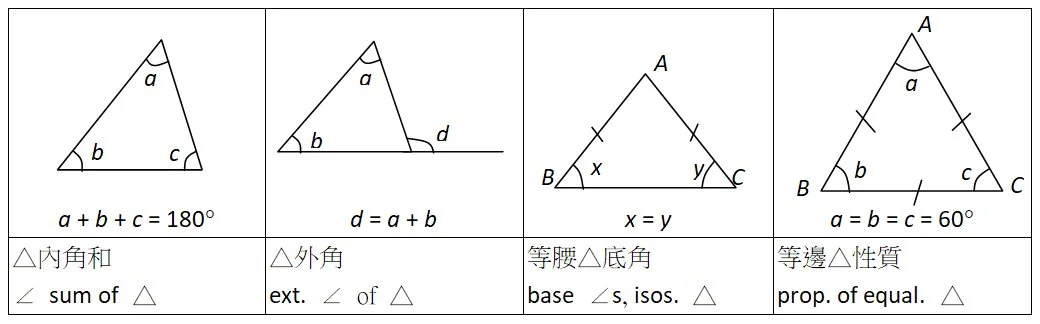



12 演繹推理幾何 與三角形有關的定理 齊齊溫



三角 反三角 函数在javascript中的应用 专注前端开发 十行笔记
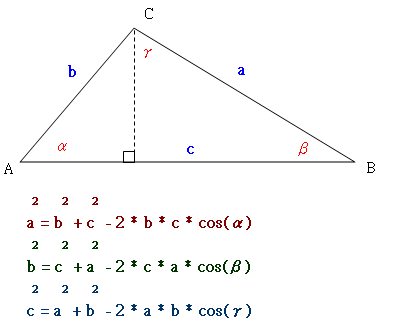



餘弦定理 Cosine Theorem Lexra Pixnet 痞客邦



21版高考数学一轮复习第四章三角函数解三角形4 6正弦定理和余弦定理练习新人教b版 淘文库
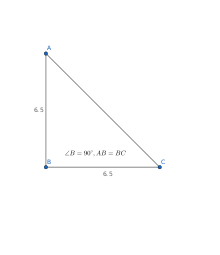



三角形 维基百科 自由的百科全书



三角恒等式




数学 三角形余弦定理证明 只布布倩 Csdn博客 余弦定理



勾股定理是谁确立的 快资讯




新中学三角体系 概述及其进一步思考 参考网
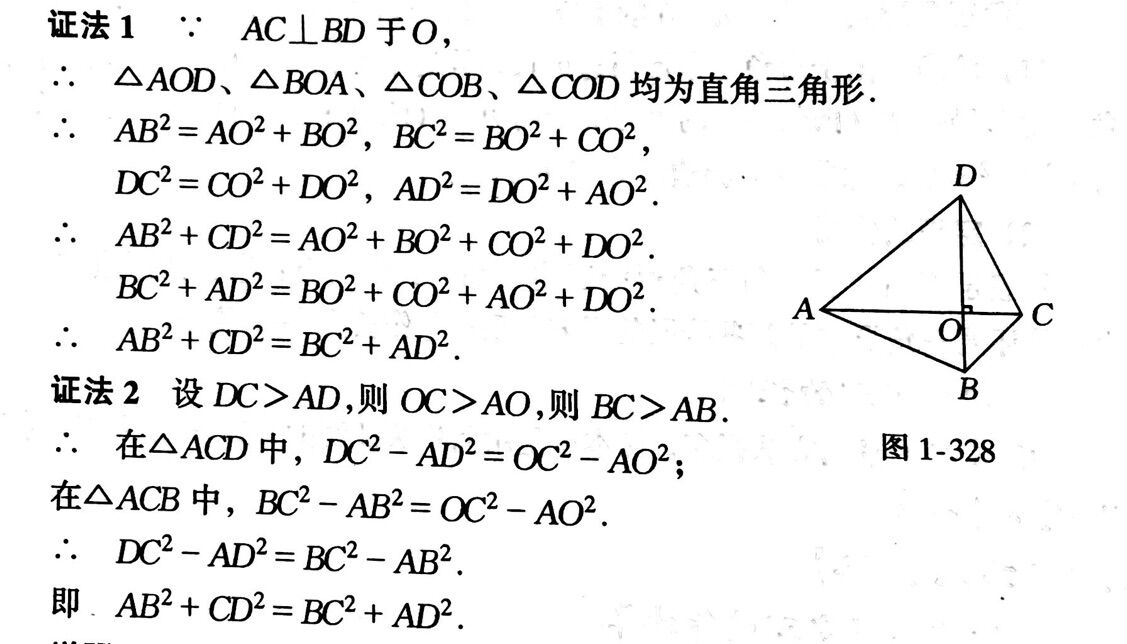



勾股定理及勾股定理的逆定理




高考数学考点之正 余弦定理及解三角形 王羽课堂




如何使用勾股定理 12 步骤



考研数学的初等函数变换公式 三角相关 知乎




怎样利用三角函数解决向量问题 勾股定理逆定理的应用 每日头条
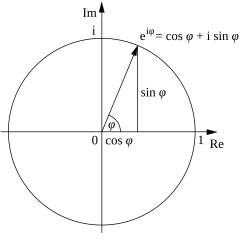



三角学 维基百科 自由的百科全书



1



勾股定理的逆定理关于勾股定理的证明过程 学习岛




相似三角形定理的证明




01利用勾股定理求边长勾股定理初中数学初二 Youtube




三角形相似与三角形的重心定理及衍生定理 正余弦定理 梅涅劳斯定理 哔哩哔哩




三角学 维基百科 自由的百科全书



斜边中线定理如何证明直角三角形斜边中线定理 不要涉及高中知识 朵拉利品网




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




餘弦定理 维基百科 自由的百科全书



三角函数余弦定理 搜狗图片搜索




高三同学看过来 学好正余弦定理的应用 为三角系列划上完美




高考数学考点之正 余弦定理及解三角形 王羽课堂




三角函数的正弦定理 三角函数正弦定理 三人行教育网 Www 3rxing Org




勾股定理的证明方法5种
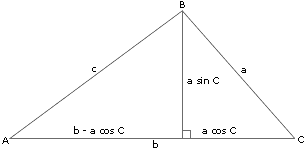



餘弦定理 维基百科 自由的百科全书
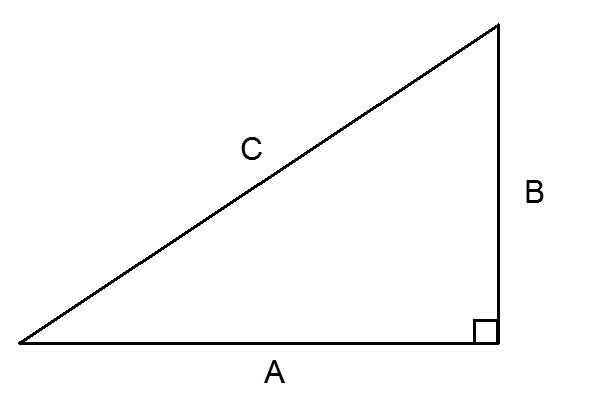



勾股弦定理 中文数学wiki Fandom
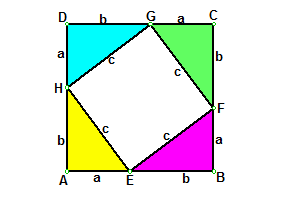



勾股定理的证明方法汇总一



初中数学 圆幂定理与相似比 中学数学研究会 微信公众号文章阅读 Wemp



几何中的ptolemy定理与两角和的三角函数 哔哩哔哩 つロ干杯 Bilibili



三角形中三角比的特殊公式 知乎



几何课关于三角形你不得不记住的定理 从勾股定理到托勒密定理




17三角函数trigonometric Function射影定理 Youtube



你知道12岁的爱因斯坦是怎么证明勾股定理的吗 新闻 蛋蛋赞



0 件のコメント:
コメントを投稿