例題 三平方の定理_座標平面の三角形 2/15 例題 三平方の定理_二等辺三角形の面積 例題 三平方の定理_台形の面積 2/14 例題 三平方の定理_最短経路 学習 コンテンツ 練習問題 各単元の要点 pcスマホ問題 数学の例題 学習アプリ 中2 連立方程式 計算問題アプリ数学 円 の性質 って 中3数学弦の長さを求める問題の解き方3ステップ 41 個の質問と回答; 正弦定理と外接円正弦定理を紹介した時に外接円については触れなかったので、ここで少し確認したいと思います。まず「外接円」とは何かというと三角形の3つの頂点全てを通る 数学を始める前に 数学Ⅰ・A 数学Ⅱ・B 数学Ⅲ 高校数学の問題と解答の部屋 教科書の問題を質問!解説依頼
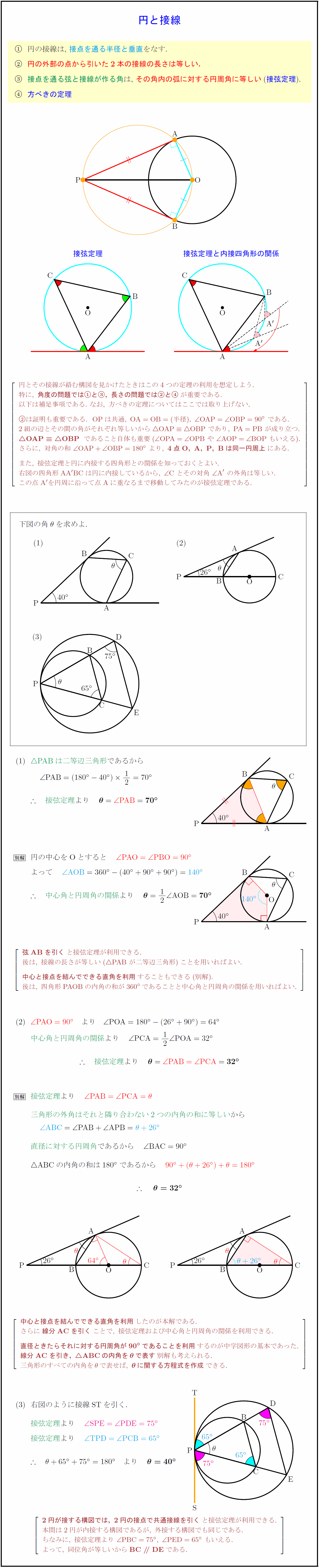
高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月
数学 円 定理
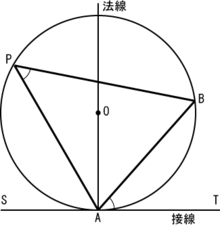
数学 円 定理- 円の外部の1点 $\mathrm{P}$ からその円に引いた2本の接線の長さは等しい。 接弦定理 円 $\mathrm{O}$ の弦 $\mathrm{AB}$ と,その端点 $\mathrm{A}$ における接線 $\mathrm{AT}$ が作る角 $\angle \mathrm{BAT}$ は,その角の内部に含まれる $\stackrel{ \Large \frown }{\mathrm{AB}}$ に対する円周角 $\angle \mathrm{ACB}$ に等しい。平面図形 接弦定理 説明 Date09年 9月30日 円に内接する があるとき, を接点とする接線と円の弦 の作る角は, その角の内部にある弦に対する円周角と等しくなります。 図で表すと, となります。 これは以下のように証明ができます。 (1) のとき,




高校数学 数a 45 円周角の定理 Youtube
接弦定理接弦定理は「円に内接する三角形とその円に接する接線があり、かつ三角形の"ある"頂点が接点となっている」場合に考えることができます。次のような状態の時ですね 数学を始める前に 数学Ⅰ・A 数学Ⅱ・B 数学Ⅲ 高校数学の問題と解答の部屋 教科書の問題を質問!解説依頼正解率 \(0\) % 岐阜県の公立高校の入試問題・数学で出題された難問です。 正解率 \(0\) %だったそうです。 難問ですが、決して意地悪な出題ではありません。 たくさんの要素がつまった良問です。 得るものが多い一題ですので、ぜひ矢onky より 17年9月16日 537 PM 円周角の証明を教えてください ken より 17年9月
数学 において、 円 (えん、 英 circle )とは、 平面 (2次元 ユークリッド空間 )上の、定点 O からの距離が等しい 点 の集合でできる 曲線 のことをいう。 ここで現れる定点 O を円の 中心 と呼ぶ。 円には、その中心が1つあり、また1つに限る。 円周角の定理はこれで完璧! 定理の証明と様々な問題の解法 中学で学習する図形を大きく分けたとき、三角形に関するもの、四角形に関するもの、円に関するもの、に大きく分類することができるでしょう。 今回学習するのは、円に関するもの円 (数学) 円 (数学)の概要 ナビゲーションに移動検索に移動この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。出典検索?
反転(円に関する鏡像変換) 円の極線の詳細は次のページにあります。 円に関する極と極線(共役定理) 定期試験・大学入試に特化した解説。 接線の公式x₁xy₁y=r²は点 (x₁,y₁)が円内外にあるとき極線を表す。 円の弦の両端を接点とする2本の接線円と三平方 弦の長さ 円の中心から弦に垂線を引くと、弦の垂直二等分線になる。 例 半径7の円で、中心から弦abまでの距離が3である。 弦abの長さを求める。 やり方 ab=xとする。 直角三角形apoで、ap= x 2 、ao=7、po=3を 三平方の定理にあてはめる。 (x 2) 2中学生からの質問(数学) や が出てくるのは,次の2つの特別な直角三角形の場合です。 直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次の




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
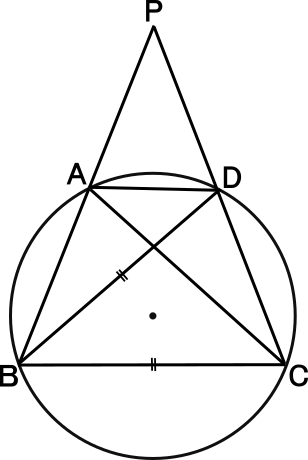



中学3年数学練習問題 円周角の定理の活用 証明問題
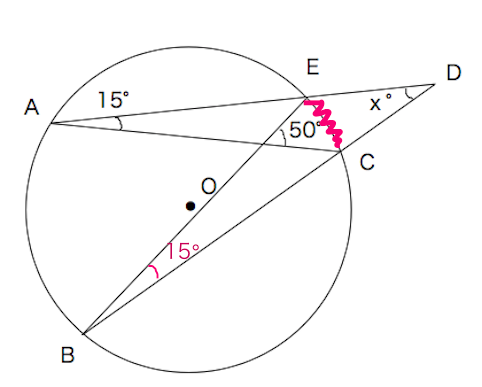
AE\times EC=BE\times ED AE × EC = BE ×E D動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru数学Aの円で使う定理・性質の一覧 円周角の定理 弧ABに対する円周角の大きさはつねに一定であり、その角の大きさは、その弧に対する中心角の大きさの半分である。 ・∠ACB=∠ADB ・∠AOB=2∠ACB=2∠ADB また、次の図のよ




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



円に関する定理や性質 わかる数学
フォイエルバッハの定理 三角形の九点円と内接円は接することを示せ.(激難) yootaamath 2149 Tweet 広告を非表示にする 関連記事 初等的解法の存在する角度の問題 日曜数学 Advent Calendar 18 の11日目の記事です。 adventar 問題コーナー(第3回)解答 この問題は定理一覧 円を含む図形 方べきの定理 トレミーの定理 シムソンの定理 シュタイナーの定理 アルハゼンの定理 ニュートンの定理 九点円の定理 フォイエルバッハの定理 ターレスの定理 パスカルの定理 アポロニウスの定理 ブリアンショの定理02/01 「有名問題・定理から学ぶ高校数学」の索引 を作成しました 用語や問題の背景から問題へジャンプできるようになっています 皆さまの受験勉強にぜひお役立てください




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名
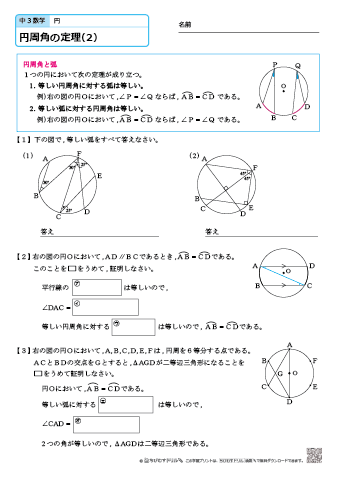
なぜ円周角の定理が成り立つのか、その証明については以下をご覧ください。 円周角の定理の証明|図で分かりやすく解説 円周角の定理は、1つの弧に対する円周角・中心角に関する定理です。 円周角の定理 1つの弧に対する円周角は等しい その円周角はそ全て完全無料の中学数学練習問題プリント 三平方の定理と円 例題 弦ABの長さを求める。 円Oの半径6cm、中心から弦ABまでの距離が2cmである。 A B O 半径6cm 2cm 円Oに点Pから引いた接線PAの長さを求める。 円Oの半径5cm、OP=10cm、Aは接点である。 A P O 半径5cm, OP=10cm ① 直角三角形AOPで三平方の① 接弦定理 中学数学の「円の性質」で最も大事なものと思われる3つのうちの 2つ目「接弦定理」ですね! 現在の公立中学では課程から外れているかもしれませんが 私立中学では必ず学んでいるはずです 接弦定理 ・ ∠b = ∠a ・ ∠t = ∠s (弦BCと接線がつくる∠bは 弧BCの円周角∠a
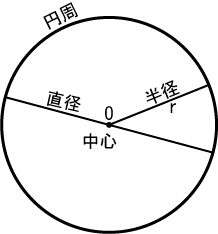



円 数学 Wikipedia
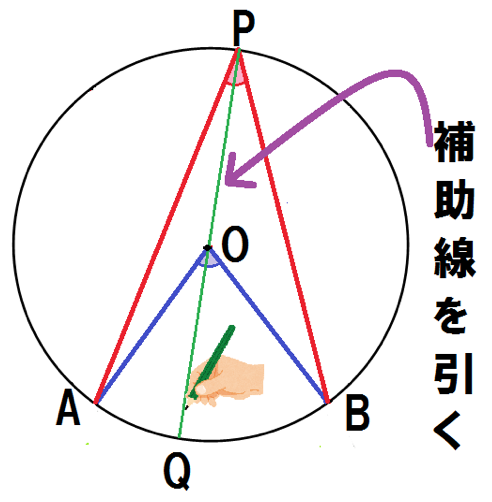



これでスッキリ 円周角の定理の証明の3つのパターン Qikeru 学びを楽しくわかりやすく
九点円の定理の証明と諸性質 九点円の定理: 三角形 a b c abc a bc において,以下の9点は同一円周上にある。 三辺の中点 a m, b m, c m a_m,b_m,c_m a m , b m , c m 垂線の足 a h, b h, c h a_h,b_h,c_h a h , b h , c h 垂心と各頂点の中点 a n, b n, c n a_n,b_n,c_n a n , b n , c n → 九点円の定理の証明と諸性質 円と相似 円と相似に関する問題です。 円周角の定理を利用して、相似な三角形の証明をしたり、相似比を利用して長さを求めたりします。 基本的な問題は難しくないのでしっかり確認しておいてください。 よくある相似の証明 1 下の図で A 16年11タレスの定理 (タレスのていり、 英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理 、 タレースの定理 ともいう。



円周角の定理 練習問題 苦手な数学を簡単に




中学3年の数学 動画 円周角の定理 基本編の問題 19ch
高校数学 Ⅰ 高校数学Ⅱ 「三平方の定理と円 」 が絡む問題をやってみよう。 ポイントは以下の通りだよ。 point 中心から弦への垂線は、垂直二等分線になる 弦ABの長さを求める問題だね。どうやって考えていこうか。 まず、ポイントを利用すると、中心Oから弦ABに引いた垂線は、ABの 垂直 外接円oの半径は、正弦定理を用いて、 7√3÷sin60°=7 であるとわかります。(今回は正弦定理の解説ではないので詳しい説明は省きます。) このとき、円周角の定理より、∠apb=60°であることがわかります。 いま、 2pa=3pbになるときのpaの長さ を求めたいので、 2pa=3pb⇔papb=32より、x>0を満たすxこの「半円の弧 A B に対する円周角 ∠ A P B は直角になる」という性質は タレスの定理 と言って、工学・建築学の世界ではよく使う性質なので、ぜひ覚えておいてください。 タレスの定理 線分 A B を直径とする円の円周上に A, B と異なる点 P をとると
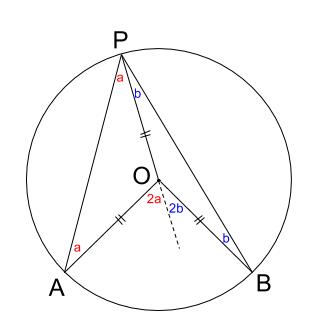



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su
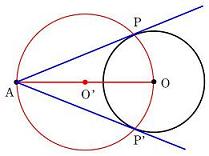



中学校数学 3年生 図形 円 Wikibooks
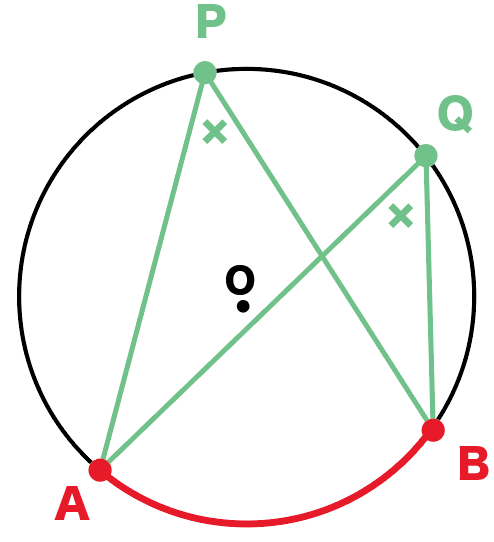
円に関する定理や性質 by omusoshiru 公開 19年7月13日 更新済み 19年7月12日 1円周角の定理 円周角の定理 円の性質。 ① 同じ弧に対する円周角は全て等しい。 ② 円周角は中心角の半分である。 円周角と弧 円の性質。 ① 弧が等しい ⇔ 円周角が等しい ② 弧の長さは円周角の大き 中1数学 四則演算正の数・負の数の計算問題の5つコツ 中3数学 三角形の比角の二等分線の定理・性質の問題の解き方がわかる3ステップ 中2数学 簡単公式平行四辺形の面積の求め方がわかる3ステップ 中2数学 153接弦定理4 円周角の定理 (入試問題) → 携帯版は別頁 弧(こ)・弦(げん)とは 円周の一部を「弧」という. 例 右図の赤で示した部分を 弧 AB などという.(これに対して灰色で示した線分は 弦 AB という.) ※ 1つの弦により円周全体は2つの弧に



1




中学3年数学練習問題 円 円周角の定理 内接円 接弦定理 の問題
中学数学 定期テスト対策円 「円周角の定理 」の基礎 円「円周角の定理」の基礎 「円周角の定理」を教えてください。 進研ゼミからの回答 「円周角の定理」では,3つのことを覚えましょう。 (2)1つの弧に対する円周角はすべて等しいです。 (3)半円の弧に対する円周角は直角円周角の定理 一つの弧に対する「円周角」の大きさは,「中心角」の半分になります. (証明) 1 右のようにACが中心を通るとき oc=ob= (半径)だから OBCは二等辺三角形になる. 二等辺三角形の2つの底角は等しいから ∠ b= ∠ c (1) 「三角形の外角は,それと隣り合わない2つの内角の和T2:円の接線にはどんな性質がありましたか。 s2:接点を通る半径に垂直です。 s3:弦が直径なので,タレスの定理が使えそうです。 ・「円の弦と,その一端を通る接線のつくる角とその角内にある弧に対する円周角」と表現できることを確認する。




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




本書で紹介する定理たち Hirosi Ooguri
三角定規を利用して円の いことを,数学的に説明す ることができる。 三角定規を利用して円の 中心をさがす方法が正し いことを説明することが できる。 円周角の定理や円の中心 の位置などについて再確 認させる。 直径と円周角の定理を理解し, それを利用して円についてのいろ 3 10 2大学の数学の勉強が始められるように、話題と本の紹介をすることを目指しました。 1 円の定義 (1) 円 は「平面上で、ある1 点から等しい距離にある点の集まり」 として定義されます。 r o (2) この説明に満足せずに、他の方法で定義(特徴付け) はできない でしょうか。例えば、次の定理は円周角の定理の応用 円の接線 まずは1年生で学んだ円の接線について復習する。 直線が円とただ1点で出あうとき、この直線は円に接する(せっする)といい、この直線を円の 接線(せっせん) といい、出あう1点を 接点(せってん) という。



1



円周角の定理と中心角 中学3年数学 Youtube
初等数学公式集 出典 フリー教科書『ウィキブックス(Wikibooks)』 ナビゲーションに移動 検索に移動 " 公式とは、数式で表される定理のことである " ( 出典フリー百科事典『ウィキペディア(Wikipedia)』 公式 ) 以下に、日本の数学教育において大学
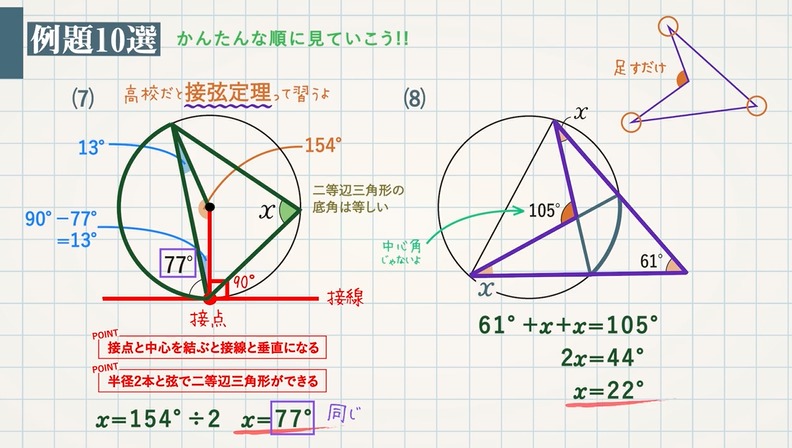



円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




中学校数学 3年生 図形 円 Wikibooks
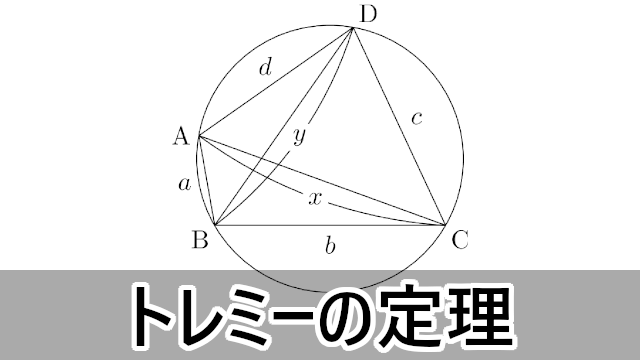



トレミーの定理 中学生も理解できる 大学入試数学の考え方と解法




円周角の定理の逆 中学3年生 円の性質 数学 Youtube



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典




数学 中3 56 円周角の定理 基本編 Youtube




補助円を使う証明問題 中学3年生の数学より 身勝手な主張




中学3年の数学 動画 円周角の定理 もっと応用編の問題 19ch




高校数学a 共円条件 4点が同一円周上にある条件 受験の月
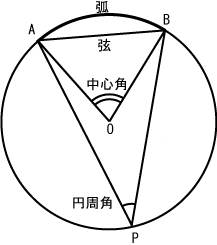



円 数学 Wikipedia
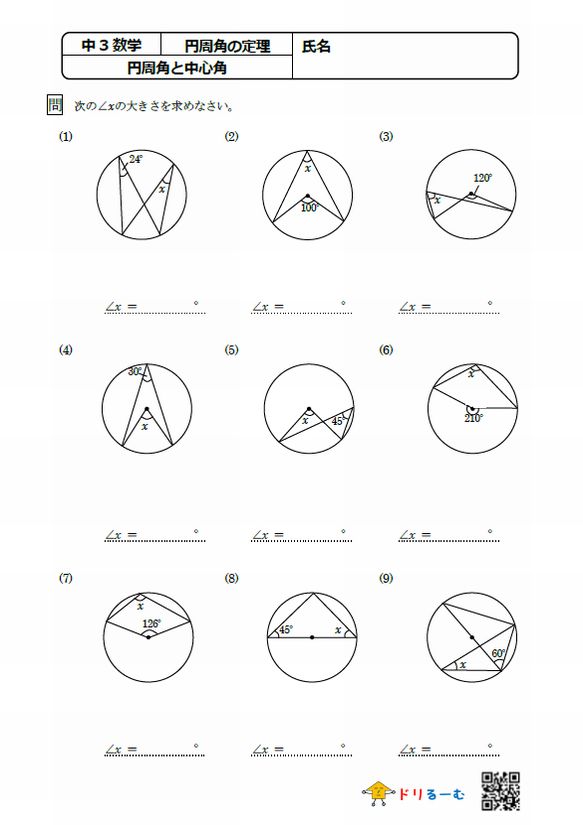



円周角と中心角 ドリるーむ
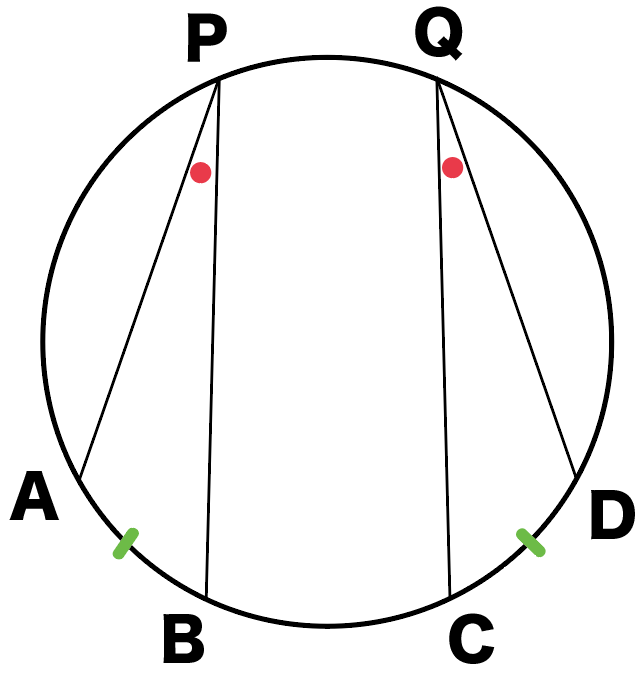



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく




中学 高校までの円に関する定理や性質をまとめました 平面図形 高校生 数学のノート Clear




勉強しよう数学 円の外の点に拡張した円周角の定理
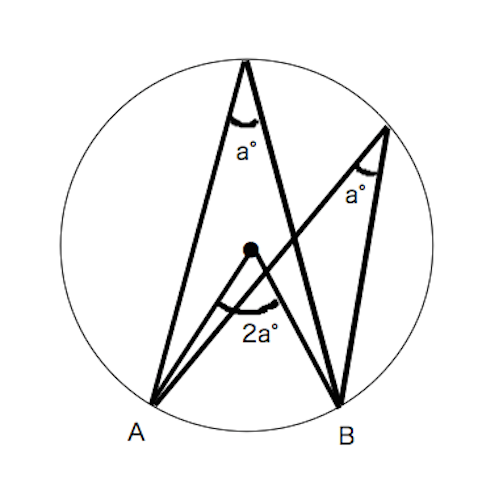



円周角の定理 苦手な数学を簡単に




中3数学 円周角の定理を使った定期テスト予想問題 Pikuu
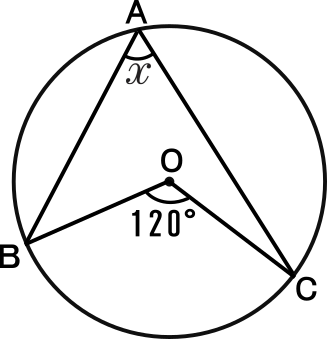



中学3年数学練習問題 円周角の定理の基本
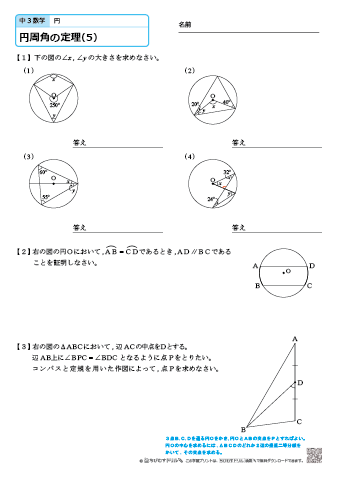



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット




中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




円周角の定理の基本 計算 無料で使える中学学習プリント




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




高校数学 数a 45 円周角の定理 Youtube




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




円周角の定理の逆 中学3年数学 Youtube




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学
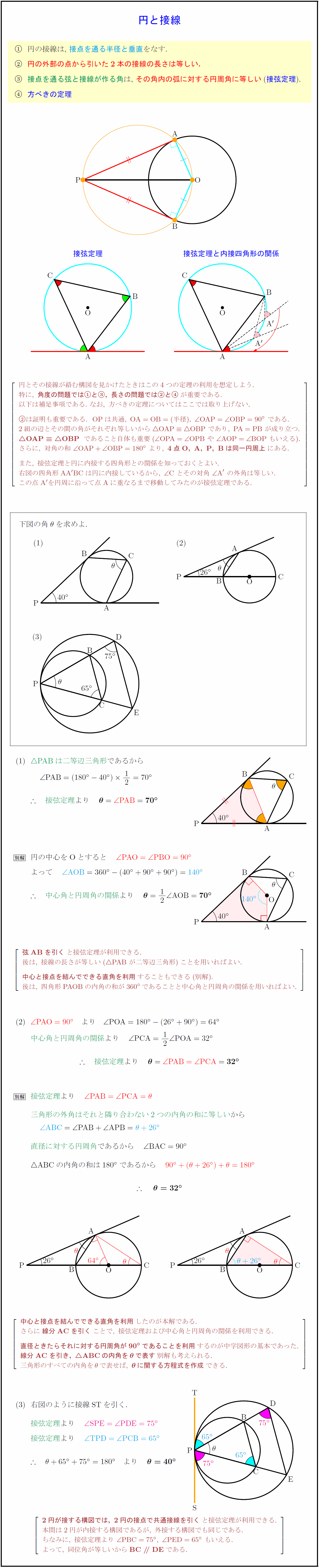



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月



中学校数学 3年生 図形 円 Wikibooks



1



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく



Studydoctor方べきの定理と考え方 高校数学a Studydoctor




円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題




中学3年 数学 円周角の定理の問題です これの解き方教えてください Clear
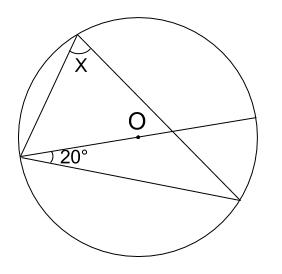



中学数学 円周角の定理 例題その3 中学数学の無料オンライン学習サイトchu Su




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
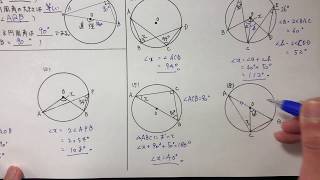



中3数学 円の性質2 円周角と中心角 すべて無料 星組の中学数学講座




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト



1




ม 3 โน ตของ 中3 数学 円周角の定理 ช น Junior Clear



数学 円周角の定理 静岡県公立高校入試問題




中3 数学 円5 円周角の定理の逆 11分 Youtube
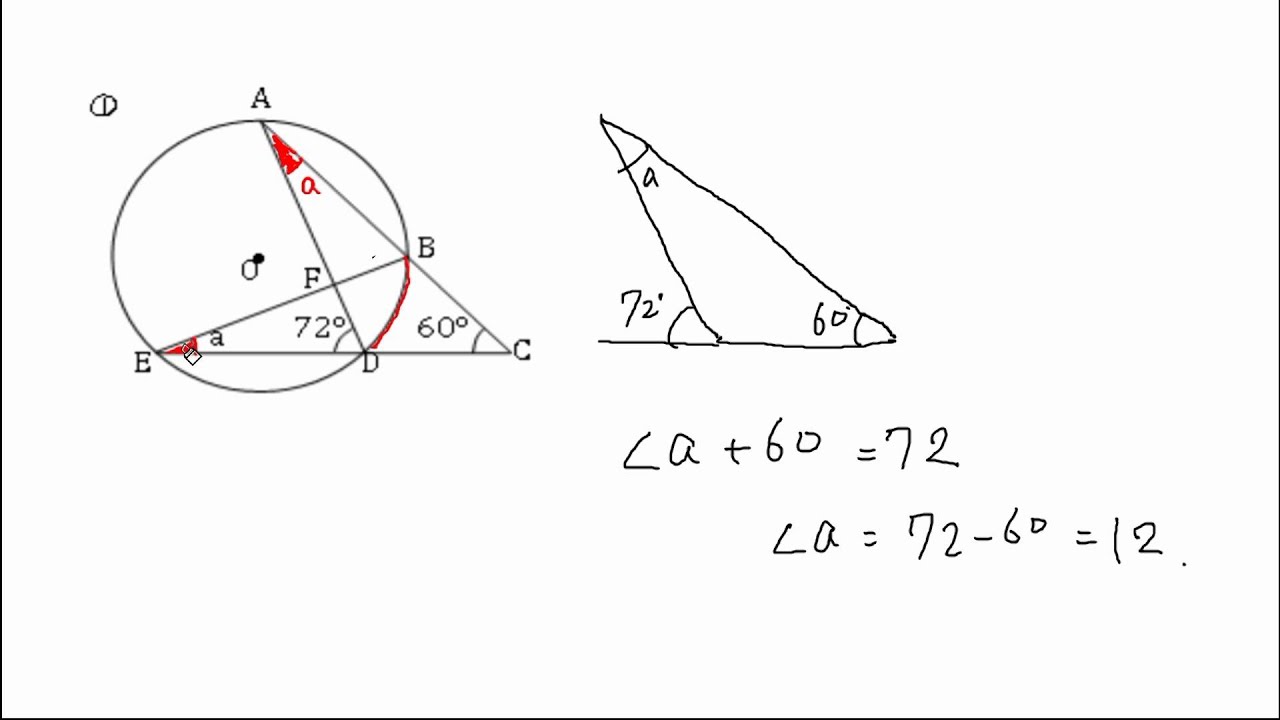



円周角の定理 問題 Youtube
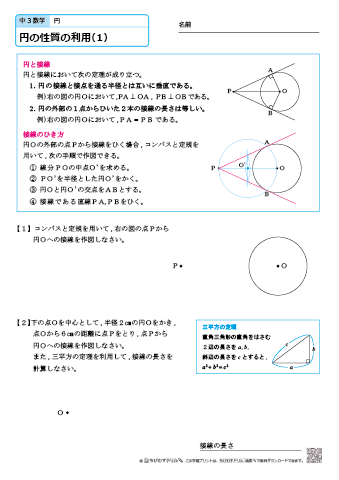



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生
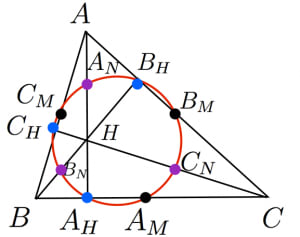



九点円の定理の証明と諸性質 高校数学の美しい物語
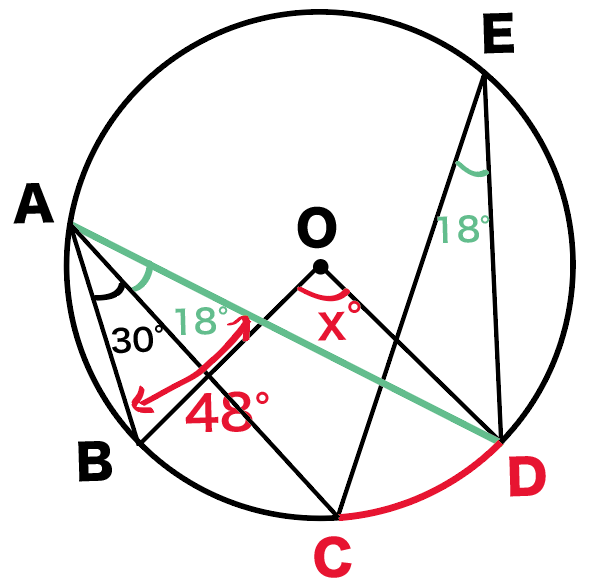



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
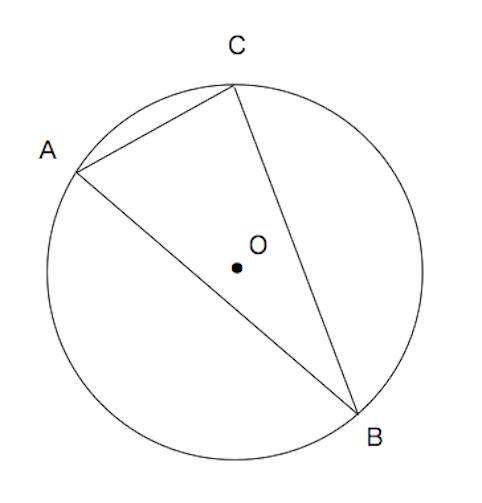



円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に
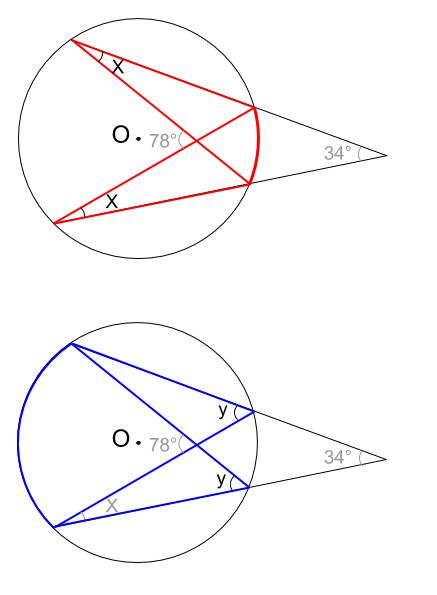



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su
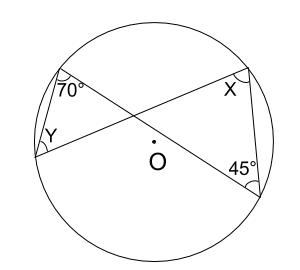



中学数学 円周角の定理 例題その1 中学数学の無料オンライン学習サイトchu Su
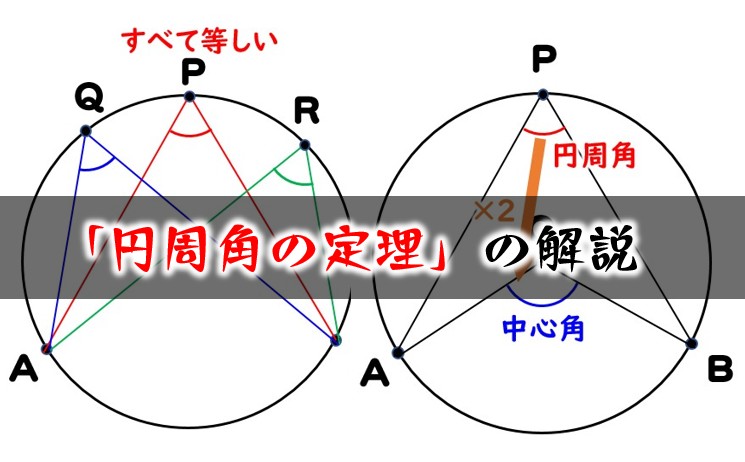



円周角の定理の解説 問題の解き方 数学fun




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
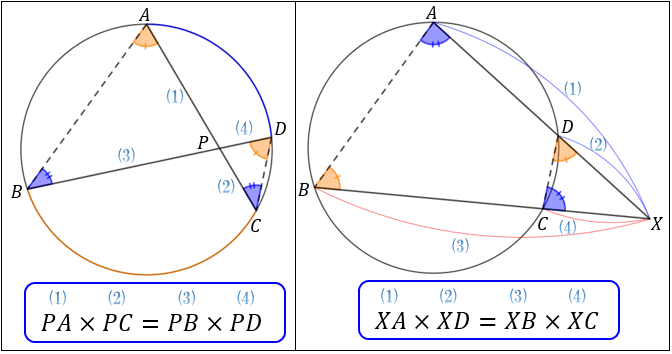



方べきの定理とは 3つのパターンの図解とその証明方法 アタリマエ
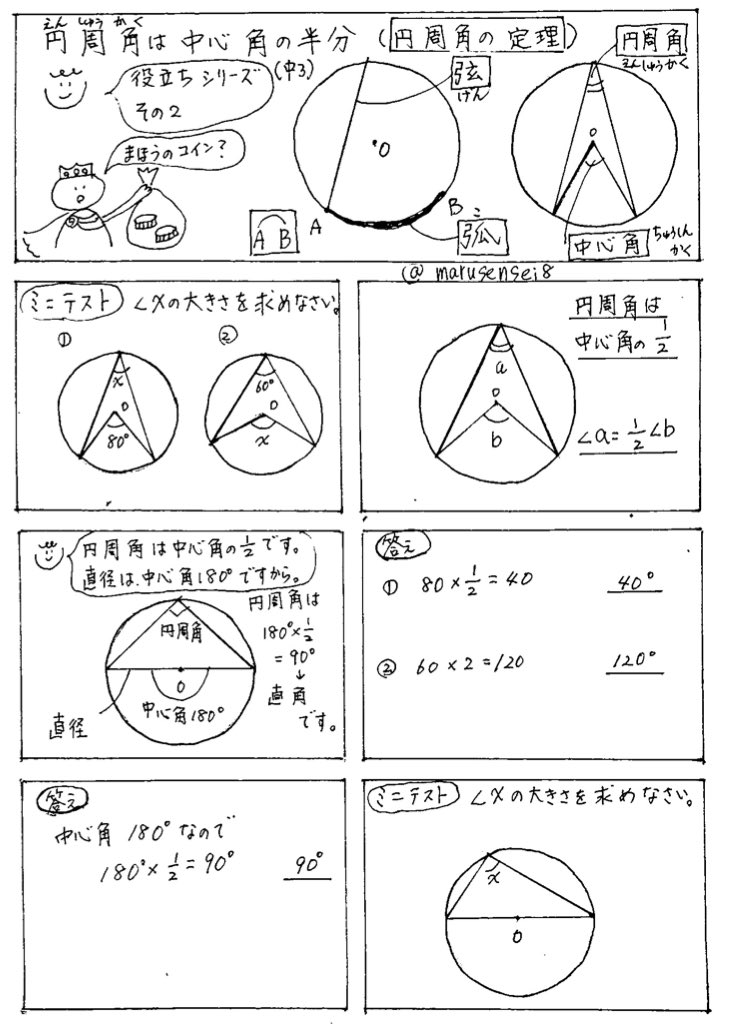



円周角の定理




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




数学 中3 57 円周角の定理 少し応用編 Youtube




中3数学 円の性質8 円周角の定理の逆 4点が同じ円周上にあることの証明 すべて無料 星組の中学数学講座




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




やさしい円周角の定理の覚え方 Schoolmath S Diary




円周角の定理の逆 無料で使える中学学習プリント




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



円の基礎知識 中学から数学だいすき




これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




中3 数学 円周角の定理 中学生 数学のノート Clear




中3数学 円周角の定理 良難問とその解説 定期テストや高校入試に レオンの中学数学探検所
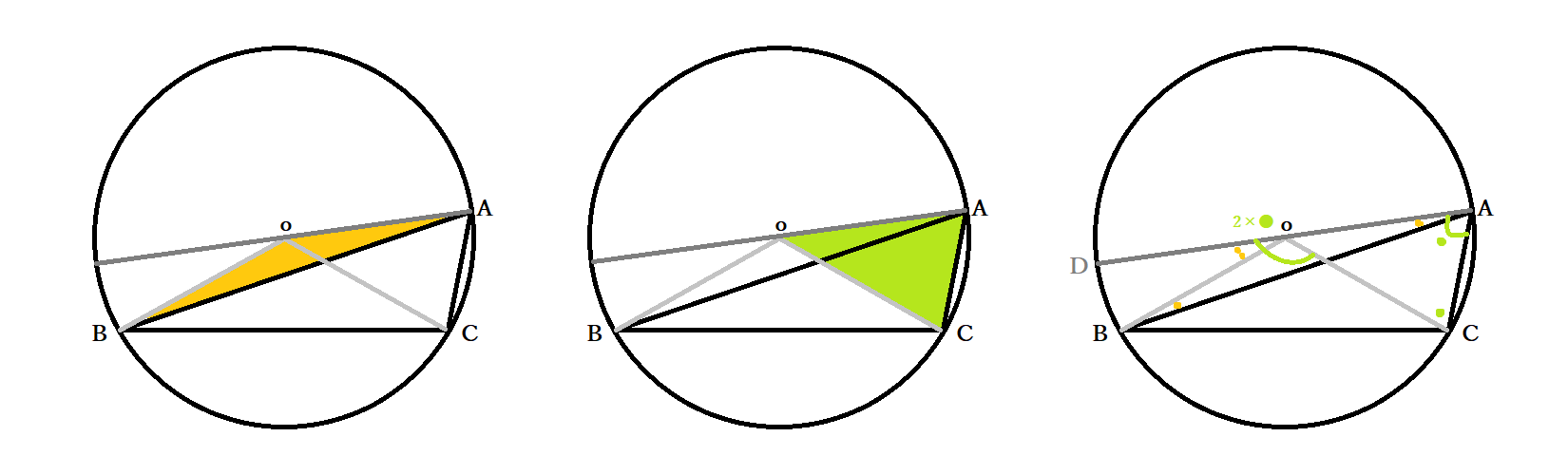



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog
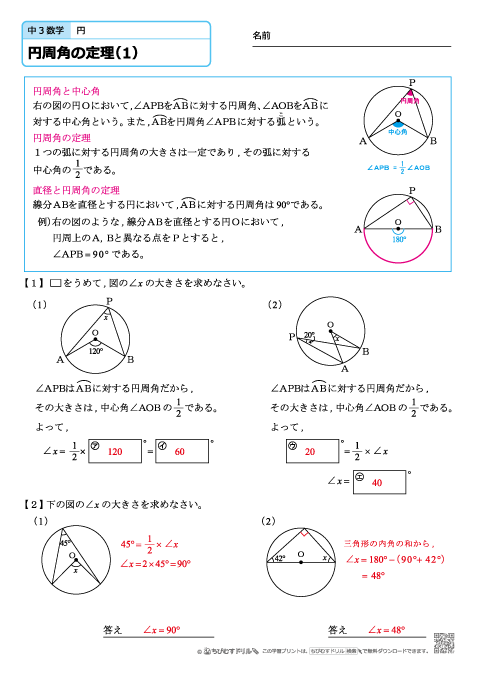



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
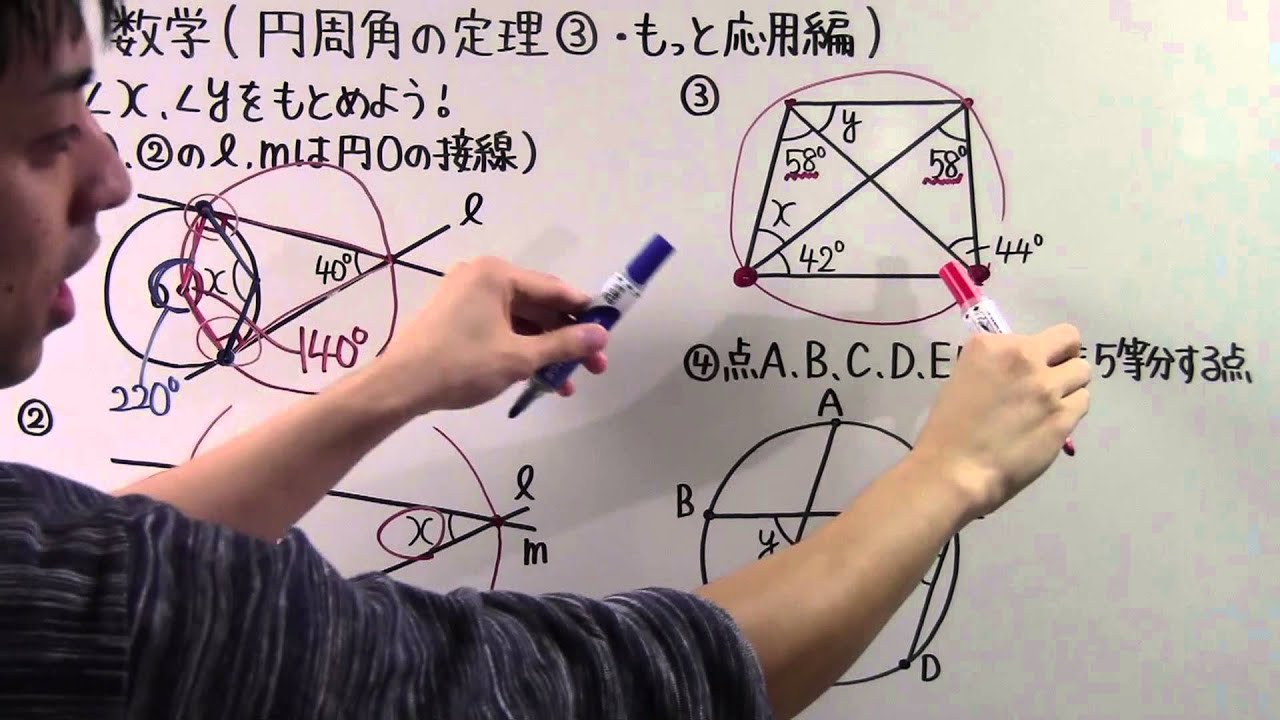



数学 中3 58 円周角の定理 もっと応用編 Youtube




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



円周角の定理
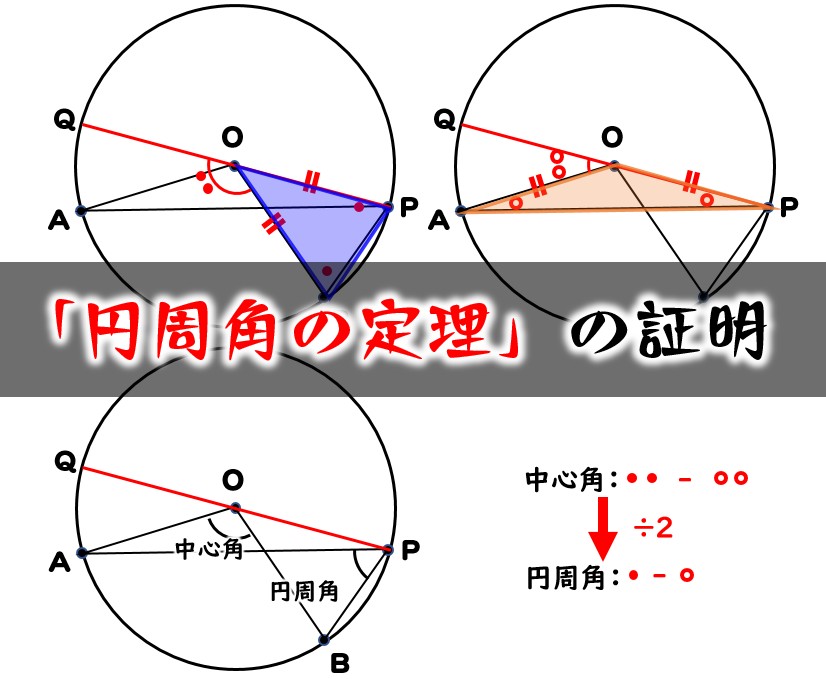



円周角の定理の証明 図で分かりやすく解説 数学fun



円 数学 Wikipedia




中学3年の数学 動画 円周角の定理 少し応用編の問題 19ch




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
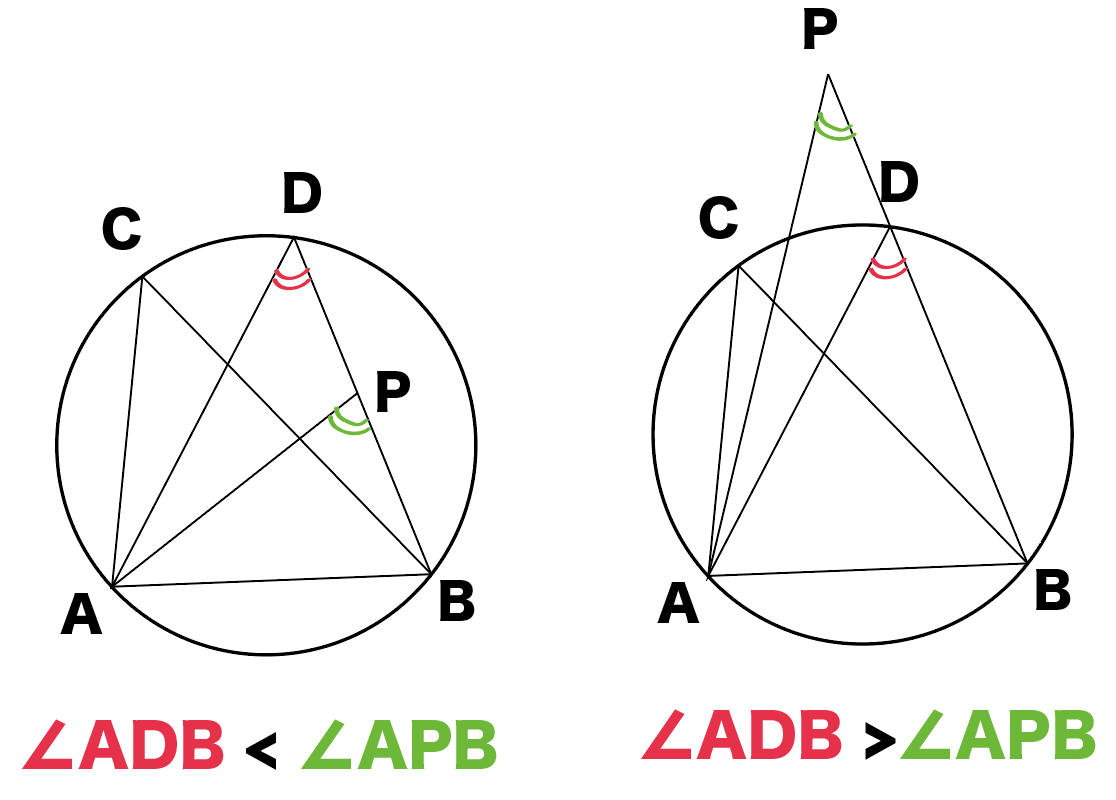



3分でわかる 円周角の定理の逆の証明 Qikeru 学びを楽しくわかりやすく




中3数学 円周角 三角形の外角の関係を使う問題 Youtube



数学a 平面図形 円の性質 方べきの定理




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
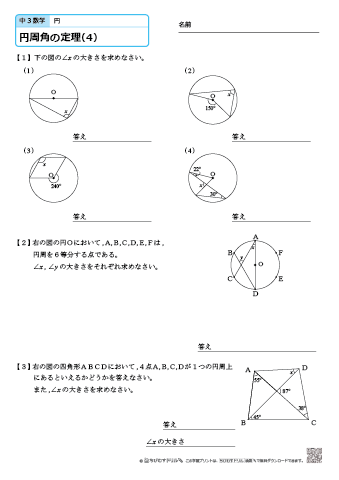



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



円周角の定理




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張



0 件のコメント:
コメントを投稿